题目内容
已知函数 .
.(Ⅰ)写出函数f(x)的定义域,并求函数f(x)的单调区间;
(Ⅱ)设过曲线y=f(x)上的点P的切线l与x轴、y轴所围成的三角形面积为S,求S的最小值,并求此时点P的坐标.
【答案】分析:(Ⅰ)根据负数没有平方根即被开方数大于等于0,列出关于x的不等式,求出不等式的解集即可得到x的取值范围即为函数的定义域,然后求出f(x)的导函数,令导函数大于0列出关于x的不等式,求出不等式的解集即可得到x的取值范围即为函数的增区间;令导函数小于0列出关于x的不等式,求出不等式的解集即可得到x的范围即为函数的减区间;
(Ⅱ)设出切点P的坐标,把横坐标代入到f(x)的导函数中求出对应的导函数值即为切线的斜率,根据设出的P的坐标和求出的斜率写出切线l的方程,然后分别令x=0和y=0求出切线l与y轴和x轴的交点坐标,根据与坐标轴的截距表示出三角形AOB的面积,化简后利用基本不等式即可求出面积的最小值和此时P的坐标.
解答:解:(Ⅰ)函数f(x)的定义域是[-2,2].
函数f(x)的导函数是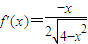 .
.
令f'(x)>0,即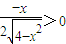 ,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);
,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);
令f'(x)<0,即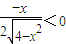 ,解得0<x<2,所以函数f(x)的递减区间是(0,2).
,解得0<x<2,所以函数f(x)的递减区间是(0,2).
(Ⅱ)设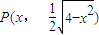 ,则切线的斜率
,则切线的斜率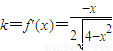 ,
,
则切线l的方程是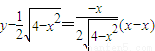 ,
,
设切线l与x轴、y轴的交点为A、B,
令y=0,由题意可知x≠0,解得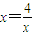 ,所以
,所以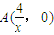 ;
;
令x=0,解得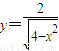 ,所以
,所以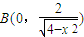 ,
,
所以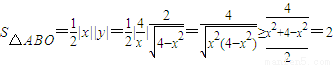 ,
,
当且仅当x2=4-x2,即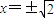 时,△ABO面积的最小值为2.
时,△ABO面积的最小值为2.
此时,点P的坐标是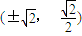 .
.
点评:此题考查学生会利用导函数的正负求出函数的单调区间,会利用基本不等式求函数的最值并掌握最值的几何意义,会利用导数求曲线上过某点切线方程的斜率,是一道多知识的综合题.
(Ⅱ)设出切点P的坐标,把横坐标代入到f(x)的导函数中求出对应的导函数值即为切线的斜率,根据设出的P的坐标和求出的斜率写出切线l的方程,然后分别令x=0和y=0求出切线l与y轴和x轴的交点坐标,根据与坐标轴的截距表示出三角形AOB的面积,化简后利用基本不等式即可求出面积的最小值和此时P的坐标.
解答:解:(Ⅰ)函数f(x)的定义域是[-2,2].
函数f(x)的导函数是
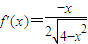 .
.令f'(x)>0,即
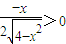 ,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);
,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);令f'(x)<0,即
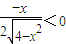 ,解得0<x<2,所以函数f(x)的递减区间是(0,2).
,解得0<x<2,所以函数f(x)的递减区间是(0,2).(Ⅱ)设
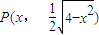 ,则切线的斜率
,则切线的斜率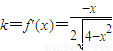 ,
,则切线l的方程是
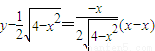 ,
,设切线l与x轴、y轴的交点为A、B,
令y=0,由题意可知x≠0,解得
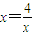 ,所以
,所以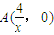 ;
;令x=0,解得
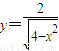 ,所以
,所以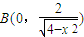 ,
,所以
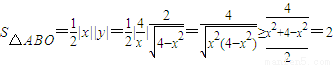 ,
,当且仅当x2=4-x2,即
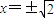 时,△ABO面积的最小值为2.
时,△ABO面积的最小值为2.此时,点P的坐标是
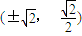 .
.点评:此题考查学生会利用导函数的正负求出函数的单调区间,会利用基本不等式求函数的最值并掌握最值的几何意义,会利用导数求曲线上过某点切线方程的斜率,是一道多知识的综合题.

练习册系列答案
相关题目
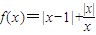 .
.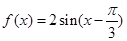 ,
,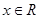 .
.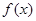 的周期;
的周期;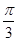 个单位,得到函数
个单位,得到函数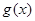 的图象,写出函数
的图象,写出函数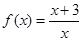 :
: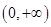 为单调递减函数;
为单调递减函数;
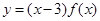 的奇偶性.
的奇偶性.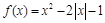 的图像,并写出该函数的单调区间与值域。
的图像,并写出该函数的单调区间与值域。 的解析式写成分段函数;
的解析式写成分段函数;