题目内容
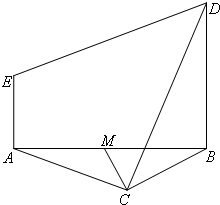
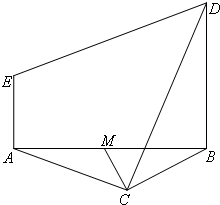 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.(1)证明:CM⊥DE;
(2)在边AC上找一点N,使CD∥平面BEN.
分析:(1)由已知中因为BC=AC,M为AB中点,我们易得CM⊥AB,又由等边△ABC与直角梯形ABDE所在平面垂直,可得CM⊥平面ABDE,进而根据线面垂直的性质,即可证明CM⊥DE;
(2)连接AD交BE于点K,连接KN,由已知中直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.我们易得KN∥CD,结合线面平行的判定定理,即可得到答案.
(2)连接AD交BE于点K,连接KN,由已知中直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.我们易得KN∥CD,结合线面平行的判定定理,即可得到答案.
解答:解:(1)证明:因为BC=AC,M为AB中点.所以CM⊥AB,
又因为平面ABC⊥平面ABDE,平面ABC∩平面ABDE=AB,CM?平面ABC,
所以CM⊥平面ABDE,
又因DE?平面ABDE,所以CM⊥DE;(7分)
(2)当
=
时,CD∥平面BEN.
连接AD交BE于点K,连接KN,
因梯形ABDE中BD∥AE,BD=2AE,
所以
=
=
,则
=
又因
=
,所以KN∥CD(14分)
又KN?平面BEN,CD?平面BEN,所以CD∥平面BEN.
又因为平面ABC⊥平面ABDE,平面ABC∩平面ABDE=AB,CM?平面ABC,
所以CM⊥平面ABDE,
又因DE?平面ABDE,所以CM⊥DE;(7分)
(2)当
| AN |
| AC |
| 1 |
| 3 |
连接AD交BE于点K,连接KN,
因梯形ABDE中BD∥AE,BD=2AE,
所以
| AK |
| KD |
| AE |
| BD |
| 1 |
| 2 |
| AK |
| AD |
| 1 |
| 3 |
又因
| AN |
| AC |
| 1 |
| 3 |
又KN?平面BEN,CD?平面BEN,所以CD∥平面BEN.
点评:本题考查的知识点是直线与平面垂直的性质及直线与平面平行的判定,线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
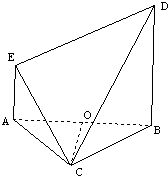 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点. 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.