题目内容
已知函数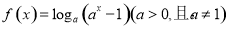
(1)求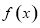 的定义域;
的定义域;
(2)当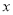 为何值时,函数值大于1.
为何值时,函数值大于1.
(1)当 时,定义域为
时,定义域为 ,当
,当 时,定义域为
时,定义域为 ;(2)当
;(2)当 时,
时, 时,函数值大于1;当
时,函数值大于1;当 时,
时, 时,函数值大于1.
时,函数值大于1.
【解析】
试题分析:(1)首先根据对数的真数大于0,然后分 与
与 两种情况求函数的定义域;(2)由不等式
两种情况求函数的定义域;(2)由不等式 分
分 与
与 两种情况进行求解.
两种情况进行求解.
试题解析:(1)由已知, ,即
,即 ,
,
当 时,
时, ,当
,当 时,
时, ,
,
∴当 时,定义域为
时,定义域为 ,当
,当 时,定义域为
时,定义域为 .
.
(2)当 时,由
时,由 得
得 ,即
,即 ,∴
,∴ ,
,
当 时,由
时,由 得
得 ,即
,即 ,∴
,∴ ,
,
∴当 时,
时, 时,函数值大于1;当
时,函数值大于1;当 时,
时, 时,函数值大于1.
时,函数值大于1.
考点:1.函数的定义域;2.对数函数的单调性;3.不等式的解法.

练习册系列答案
相关题目