题目内容
已知甲、乙两地的公路线长400千米,用10辆汽车从甲地向乙地运送一批物资,假设汽车以v千米/小时的速度直达乙地,为了某种需要,两汽车间距不得小于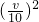 千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是________小时.
千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是________小时.
12
分析:设所需的时间为y小时,首先根据题意,得10辆车的间距和加上400正是汽车行驶的路程,再用这个路程除以速度即可求得所需的时间y的关系式,进而利用均值不等式求得y的最小值,得出需要的最少时间.
解答:设这批货物到达目的地的所用时间为y小时
因为不计汽车的身长,所以设汽车为一个点,
可知最前的点与最后的点之间距离最小值为9×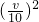 千米时,时间最快.
千米时,时间最快.
则这批物资全部到达乙地的时间y=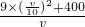 =
=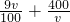 ≥
≥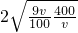 =12
=12
当且仅当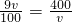 即v=
即v= 千米/小时,时间ymin=12小时
千米/小时,时间ymin=12小时
故答案为:12.
点评:本题函数模型的选择与应用,主要考查了基本不等式在最值问题中的应用,属于中档题.
分析:设所需的时间为y小时,首先根据题意,得10辆车的间距和加上400正是汽车行驶的路程,再用这个路程除以速度即可求得所需的时间y的关系式,进而利用均值不等式求得y的最小值,得出需要的最少时间.
解答:设这批货物到达目的地的所用时间为y小时
因为不计汽车的身长,所以设汽车为一个点,
可知最前的点与最后的点之间距离最小值为9×
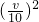 千米时,时间最快.
千米时,时间最快.则这批物资全部到达乙地的时间y=
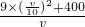 =
=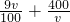 ≥
≥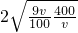 =12
=12当且仅当
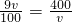 即v=
即v= 千米/小时,时间ymin=12小时
千米/小时,时间ymin=12小时故答案为:12.
点评:本题函数模型的选择与应用,主要考查了基本不等式在最值问题中的应用,属于中档题.

练习册系列答案
相关题目
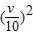 千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是 小时.
千米(汽车车身长度不计),则这批物资全部到达乙地的最短时间是 小时.