题目内容
已知函数
(1)若 从集合{0,1,2,3}中任取一个元素,
从集合{0,1,2,3}中任取一个元素, 从集合{0,1,2}中任取一个元素,求方程
从集合{0,1,2}中任取一个元素,求方程 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若 从区间[0,2]中任取一个数,
从区间[0,2]中任取一个数, 从区间[0,3]中任取一个数,求方程
从区间[0,3]中任取一个数,求方程 没有实根的概率.
没有实根的概率.
(1)  ;(2)
;(2)  .
.
解析试题分析:(1)∵ 取集合{0,1,2,3}中任一个元素,
取集合{0,1,2,3}中任一个元素, 取集合{0,1,2}中任一个元素,
取集合{0,1,2}中任一个元素,
∴ ,
, 的取值的情况有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)(3,0),(3,1),(3,2).其中第一个数表示
的取值的情况有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)(3,0),(3,1),(3,2).其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值,即基本事件总数为12.
的取值,即基本事件总数为12.
设“方程f(x)=0有两个不相等的实根”为事件A,
当a≥0,b≥0时,方程 有两个不相等实根的充要条件为a>2b.
有两个不相等实根的充要条件为a>2b.
当a>2b时,a,b取值的情况有(1,0),(2,0),(3,0),(3,1),
即A包含的基本事件数为4,
∴方程 有两个不相等实根的概率
有两个不相等实根的概率 6分
6分
(2)∵a从区间[0,2]中任取一个数,b从区间[0,3]中任取一个数,则试验的全部结果构成区域Ω={(a,b)|0≤a≤2,0≤b≤3},
这是一个矩形区域,其面积SΩ=2×3=6.
设“方程 没有实根”为事件B,则事件B所构成的区域为
没有实根”为事件B,则事件B所构成的区域为
M={(a,b)|0≤a≤2,0≤b≤3,a<2b},
它所表示的部分为梯形,其面积
由几何概型的概率计算公式可得方程 没有实根的概率
没有实根的概率 12分
12分
考点:几何概型;古典概型。
点评:做概率的有关问题,我们首相要弄清是几何概型还是古典概型,然后再代入相应的公式。属于基础题型。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,
, ,
, 时,求
时,求 ;
; ,求负数
,求负数 的取值范围.
的取值范围. ,
, ,
, ,求实数
,求实数 的值;
的值; ,求实数
,求实数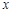 的不等式
的不等式 的解集是
的解集是 ,
, 的定义域是
的定义域是 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,集合
,集合 ,
, ,
, .
. 是集合A的子集,求实数k的取值范围.
是集合A的子集,求实数k的取值范围. ,求
,求 的值。
的值。 },
}, ,若
,若 ,求实数
,求实数 的取值范围。
的取值范围。 ,B=
,B= .
. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数 ,集合
,集合 ,集合
,集合 ,求
,求 ,
,