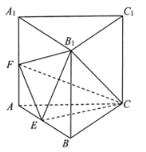
题目内容
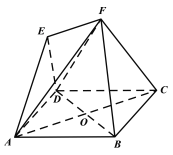
【题目】如图,正三棱柱柱![]() 中底面边长为2,高为3,DE分别在
中底面边长为2,高为3,DE分别在![]() 与
与![]() 上,且
上,且![]() .
.
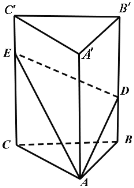
(1)AE上是否存在一点P,使得![]() 面
面![]() ?若不存在,说明理由;若存在,指出P的位置;
?若不存在,说明理由;若存在,指出P的位置;
(2)求点![]() 到截面ADE的距离.
到截面ADE的距离.
【答案】(1)存在;P为AE中点.(2)![]()
【解析】
(1)取AE中点P,AC中点Q,连接PQDP、BQ,证明四边形BDPQ为平行四边形推出![]() ,再证明
,再证明![]() 面
面![]() ,即可得出结论;(2)求出
,即可得出结论;(2)求出![]() 、
、![]() ,利用等体积法表示出
,利用等体积法表示出![]() ,即可求得
,即可求得![]() 到截面ADE的距离.
到截面ADE的距离.
(1)P为AE中点时![]() 面
面![]() ,
,
如图所示,取AE中点P,AC中点Q,连接PQDP、BQ,
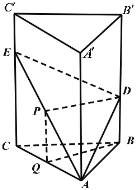
易得![]() ,
,![]() ,
,
因为P、Q分别为AE、AC中点,所以![]() ,
,![]() ,
,
所以![]() 且BD=QP,则四边形BDPQ为平行四边形,所以
且BD=QP,则四边形BDPQ为平行四边形,所以![]() ,
,
由正棱柱知:![]() 面ABC,因为
面ABC,因为![]() 平面ABC,
平面ABC,
所以![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() ,
,
由![]() 得
得![]() 面
面![]() ;
;
(2)设点![]() 到截面ADE的距离为d,
到截面ADE的距离为d,![]() ,
,
![]() ,
,
由![]()

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目