题目内容
-个冰球,在融化时其半径的减小量与时间成正比.已知从受热开始,经过2小时,融化了其体积的| 1 |
| 4 |
| 3 | 0.75 |
分析:若设冰球原来的半径为R,体积为V,则V=
πR3①;2小时后,冰球融化了其体积的
,设此时的半径为r,则体积为
V=
πr3②;
,得
=
;由参考数据,得
=0.91,即r=0.91R;由经过2小时,冰球半径的改变量△r与时间成正比,可得剩余的冰球融化完毕后所需的时间.
| 4 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
| ② |
| ① |
| 3 |
| 4 |
| r3 |
| R3 |
| r |
| R |
解答:解:设冰球原来的半径为R,体积为V,则V=
πR3①;
2小时后,冰球融化了其体积的
,设半径为r,体积为:
V=
πr3②;
由
,得
=
;由参考数据:
=0.91,得
=0.91,即r=0.91R;
则经过2小时,冰球半径的改变量△r=R-r=R-0.91R=0.09R;
设剩余的冰球t小时后融化完毕,则
=
,∴t≈20(小时);
故答案为:20.
| 4 |
| 3 |
2小时后,冰球融化了其体积的
| 1 |
| 4 |
| 3 |
| 4 |
| 4 |
| 3 |
由
| ② |
| ① |
| 3 |
| 4 |
| r3 |
| R3 |
| 3 | 0.75 |
| r |
| R |
则经过2小时,冰球半径的改变量△r=R-r=R-0.91R=0.09R;
设剩余的冰球t小时后融化完毕,则
| t |
| 2 |
| 0.91R |
| 0.09R |
故答案为:20.
点评:本题利用球的体积公式模型,考查了一个比例的应用,重点是球体积公式的灵活应用,属于基础题.

练习册系列答案
相关题目
 ,则剩余部分还需________小时融化完(精确到1小时,参考数据:
,则剩余部分还需________小时融化完(精确到1小时,参考数据: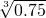 =0.91)
=0.91) ,则剩余部分还需 小时融化完(精确到1小时,参考数据:
,则剩余部分还需 小时融化完(精确到1小时,参考数据: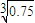 =0.91)
=0.91)