题目内容
证明下面两个命题:(1)在所有周长相等的矩形中,只有正方形的面积最大;
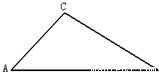
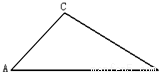
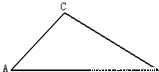
(2)余弦定理:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则a2=b2+c2-2bccosA.
【答案】分析:(1)(法一):设长方形的长,宽分别为a,b,由题设a+b为常数,结合基本不等式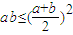 可证
可证
(法二):设长方形的周长为l,长为x,则宽为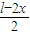 ,从而可表示长方形的面积S=x
,从而可表示长方形的面积S=x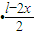 =
=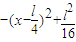 ,利用二次函数的性质可证
,利用二次函数的性质可证
(2)(法一):根据向量的数量积的性质可知,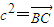
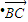 =
=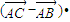 (
(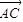
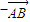 ),整理即可
),整理即可
法二:以A为原点,AB所在直线为x轴建立直角坐标系,则C(bcosA,bsinA),B(c,0),而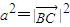 =(bcosA-c)2+(bsinA)2即可
=(bcosA-c)2+(bsinA)2即可
法三:过AB边上的高CD,则由勾股定理可得a2=BC2=CD2+BD2=(bsinA)2+(c-acosA)2,可证
解答: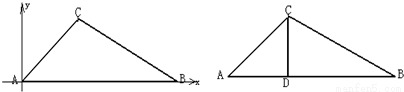 证明一:(1)设长方形的长,宽分别为a,b,由题设a+b为常数(1分)
证明一:(1)设长方形的长,宽分别为a,b,由题设a+b为常数(1分)
由基本不等式: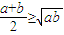 ,可得:
,可得: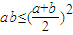 ,(4分)
,(4分)
当且仅当a=b时,等号成立,(1分)
即当且仅当长方形为正方形时,面积ab取得最大值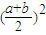 . (1分)
. (1分)
证明二:(1)设长方形的周长为l,长为x,则宽为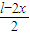 (1分)
(1分)
于是,长方形的面积S=x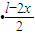 =
=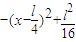 ,(4分)
,(4分)
所以,当且仅x= 时,面积最大为
时,面积最大为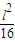 ,此时,长方形的
,此时,长方形的 ,即为正方形(2分)
,即为正方形(2分)
(2)证法一: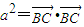 =
= (4分)
(4分)
=
=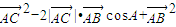
=b2+c2-2bccosA.
故,a2=b2+c2-2bccosA.(4分)
证法二 已知△ABC中A,B,C所对边分别为a,b,c
以A为原点,AB所在直线为x轴建立直角坐标系,
则C(bcosA,bsinA),B(c,0),(4分)
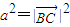 =(bcosA-c)2+(bsinA)2
=(bcosA-c)2+(bsinA)2
a2=b2+c2-2bccosA.(4分).
故,a2=b2+c2-2bccosA.(4分).
证法三 过AB边上的高CD,则a2=BC2=CD2+BD2
=(bsinA)2+(c-acosA)2
∴a2=b2+c2-2bccosA.
故a2=b2+c2-2bccosA.(4分)
点评:本题主要考查了基本不等式及二次函数的性质在求解函数最值中的应用,及三角形中的余弦定理的证明,注意本题多种解法的应用.
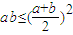 可证
可证(法二):设长方形的周长为l,长为x,则宽为
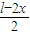 ,从而可表示长方形的面积S=x
,从而可表示长方形的面积S=x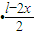 =
=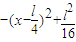 ,利用二次函数的性质可证
,利用二次函数的性质可证(2)(法一):根据向量的数量积的性质可知,
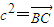
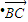 =
=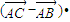 (
(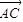
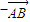 ),整理即可
),整理即可法二:以A为原点,AB所在直线为x轴建立直角坐标系,则C(bcosA,bsinA),B(c,0),而
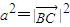 =(bcosA-c)2+(bsinA)2即可
=(bcosA-c)2+(bsinA)2即可法三:过AB边上的高CD,则由勾股定理可得a2=BC2=CD2+BD2=(bsinA)2+(c-acosA)2,可证
解答:
 证明一:(1)设长方形的长,宽分别为a,b,由题设a+b为常数(1分)
证明一:(1)设长方形的长,宽分别为a,b,由题设a+b为常数(1分)由基本不等式:
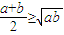 ,可得:
,可得: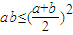 ,(4分)
,(4分)当且仅当a=b时,等号成立,(1分)
即当且仅当长方形为正方形时,面积ab取得最大值
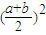 . (1分)
. (1分)证明二:(1)设长方形的周长为l,长为x,则宽为
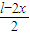 (1分)
(1分)于是,长方形的面积S=x
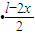 =
=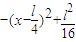 ,(4分)
,(4分)所以,当且仅x=
 时,面积最大为
时,面积最大为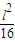 ,此时,长方形的
,此时,长方形的 ,即为正方形(2分)
,即为正方形(2分)(2)证法一:
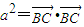 =
= (4分)
(4分)=

=
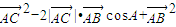
=b2+c2-2bccosA.
故,a2=b2+c2-2bccosA.(4分)
证法二 已知△ABC中A,B,C所对边分别为a,b,c
以A为原点,AB所在直线为x轴建立直角坐标系,
则C(bcosA,bsinA),B(c,0),(4分)
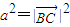 =(bcosA-c)2+(bsinA)2
=(bcosA-c)2+(bsinA)2a2=b2+c2-2bccosA.(4分).
故,a2=b2+c2-2bccosA.(4分).
证法三 过AB边上的高CD,则a2=BC2=CD2+BD2
=(bsinA)2+(c-acosA)2
∴a2=b2+c2-2bccosA.
故a2=b2+c2-2bccosA.(4分)
点评:本题主要考查了基本不等式及二次函数的性质在求解函数最值中的应用,及三角形中的余弦定理的证明,注意本题多种解法的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•闸北区一模)证明下面两个命题:
(2012•闸北区一模)证明下面两个命题: