题目内容
已知椭圆E的右焦点F2与抛物线y2=4
x的焦点重合,对称轴为坐标轴,且经过点A(1,
).
(1)求椭圆E的方程;
(2)过点D(0,
)且斜率存在的直线l交椭圆E于M、N两点,线段MN的中点为Q,点B(-1,0),当l⊥QB时,求直线l的方程.
| 3 |
| ||
| 2 |
(1)求椭圆E的方程;
(2)过点D(0,
| 5 |
| 3 |
分析:(1)设出椭圆方程,利用椭圆E的右焦点F2与抛物线y2=4
x的焦点重合,经过点A(1,
),建立方程,求得几何量,即可求出椭圆E的方程;
(2)设出直线方程与椭圆方程联立,利用韦达定理及l⊥QB,即可求直线l的方程.
| 3 |
| ||
| 2 |
(2)设出直线方程与椭圆方程联立,利用韦达定理及l⊥QB,即可求直线l的方程.
解答:解:(1)设椭圆E的方程为
+
=1(a>b>0)
∵抛物线y2=4
x的焦点为(
,0),∴F2(
,0),∴a2-b2=3①--------(3分)
又过点A(1,
),∴
+
=1②
由①,②得:a2=4,b2=1
∴椭圆E的方程为
+y2=1-----(5分)
(2)设直线l的方程为:y=kx+
(k≠0)
由
得(9+36k2)x2+120kx+64=0
由△=14400k2-256(9+36k2)>0得:k2>
设M(x1,y1),N(x2,y2),Q(x0,y0)则
----(9分)
∵l⊥QB,∴
=
=-
,化简得:4k2-5k+1=0
解得:k=1或k=
(舍去)
∴直线l的方程为y=x+
-----(12分)
| x2 |
| a2 |
| y2 |
| b2 |
∵抛物线y2=4
| 3 |
| 3 |
| 3 |
又过点A(1,
| ||
| 2 |
| 1 |
| a2 |
| 3 |
| 4b2 |
由①,②得:a2=4,b2=1
∴椭圆E的方程为
| x2 |
| 4 |
(2)设直线l的方程为:y=kx+
| 5 |
| 3 |
由
|
由△=14400k2-256(9+36k2)>0得:k2>
| 4 |
| 9 |
设M(x1,y1),N(x2,y2),Q(x0,y0)则
|
∵l⊥QB,∴
| k | QB |
| ||
|
| 1 |
| k |
解得:k=1或k=
| 1 |
| 4 |
∴直线l的方程为y=x+
| 5 |
| 3 |
点评:本题考查抛物线的性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,正确运用韦达定理是关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
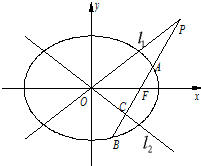 已知椭圆E的方程为
已知椭圆E的方程为 已知椭圆E的右焦点F(1,0),右准线l:x=4,离心率e=
已知椭圆E的右焦点F(1,0),右准线l:x=4,离心率e= 已知椭圆
已知椭圆 的半径等于椭圆E:
的半径等于椭圆E: (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
 .
.