题目内容
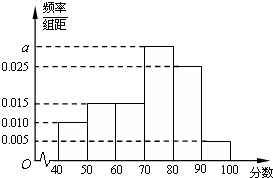
为了增强学生的环境意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理得到的频率分布直方图.
(I)若图中第一组(成绩为[40,50))对应矩形高是第六组(成绩为[90,100))对应矩形高的一半,试求第一组、第六组分别有学生多少人?
(II)在(Ⅰ)的条件下,若从第一组中选出一名学生,从第六组中选出2名学生,共3名学生召开座谈会,求第一组中学生A1和第六组中学生B1同时被选中的概率?

(I)若图中第一组(成绩为[40,50))对应矩形高是第六组(成绩为[90,100))对应矩形高的一半,试求第一组、第六组分别有学生多少人?
(II)在(Ⅰ)的条件下,若从第一组中选出一名学生,从第六组中选出2名学生,共3名学生召开座谈会,求第一组中学生A1和第六组中学生B1同时被选中的概率?

(Ⅰ)由频率分布直方图可知第一组和第六组的频率为
1-(0.006+0.024+0.028+0.030)=0.12
又由题知,第一组与第六组频率之比为1:2,所以两组频率分别为0.04、0.08
所以这两组别有学生人数为50×0.04=2人,50×0.08=4人
(Ⅱ)记[40,50)中的学生为A1、A2,[90,100)中的学生为B1、B2、B3、B4,由题意可得,基本事件为:A1B1B2,A1B1B3,A1B1B4,A1B2B3,A1B2B4,A1B3B4,A2B1B2,A2B1B3,A2B1B4,A2B2B3,A2B2B4,A2B3B4共12个
事件“A1B1同时被选中”发生有:A1B1B2,A1B1B3,A1B1B4三个,所以由古典概型知,P(A)=
=
1-(0.006+0.024+0.028+0.030)=0.12
又由题知,第一组与第六组频率之比为1:2,所以两组频率分别为0.04、0.08
所以这两组别有学生人数为50×0.04=2人,50×0.08=4人
(Ⅱ)记[40,50)中的学生为A1、A2,[90,100)中的学生为B1、B2、B3、B4,由题意可得,基本事件为:A1B1B2,A1B1B3,A1B1B4,A1B2B3,A1B2B4,A1B3B4,A2B1B2,A2B1B3,A2B1B4,A2B2B3,A2B2B4,A2B3B4共12个
事件“A1B1同时被选中”发生有:A1B1B2,A1B1B3,A1B1B4三个,所以由古典概型知,P(A)=
| 3 |
| 12 |
| 1 |
| 4 |

练习册系列答案
相关题目