题目内容
已知复数z=cos2α+isinα,α∈R,且argz=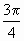 ,
,
(Ⅰ)求复数z;
(Ⅱ)若复数ω满足|ω|=1,且|z-ω|≤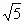 ,求argω的范围.
,求argω的范围.
答案:
解析:
解析:
|
本小题主要考查复数的概念和三角基本运算. 解:(Ⅰ)由argz= ∴2sin2α-sinα-1=0, 解得sinα=- ∵sinα>0,∴舍去sinα=- 故z=-1+i. (Ⅱ)由|ω|=1可设ω=cosθ+isinθ, 得z-ω=(-1-cosθ)+(1-sinθ)i, ∴|z-ω|= ∵|z-ω|≤ ∴3+2 又θ=argω∈[0,2π), ∴ 于是0≤θ≤ |

练习册系列答案
相关题目
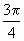 ,得cos2α=-sinα,且sinα>0
,得cos2α=-sinα,且sinα>0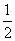 或sinα=1.
或sinα=1.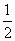 ,于是sinα=1,cos2α=-1.
,于是sinα=1,cos2α=-1.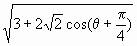 .
.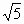 且3+2
且3+2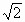
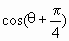 >0恒成立,
>0恒成立,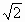
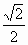 .
.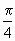 ≤θ+
≤θ+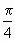 ≤
≤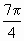 ,
,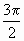 ,即 argω∈[0,
,即 argω∈[0, ].
].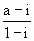 其中a>0,i为虚数单位.复数u=z(z+i)的虚部减去它的实部所得的差等于
其中a>0,i为虚数单位.复数u=z(z+i)的虚部减去它的实部所得的差等于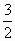 ,求复数u的模.
,求复数u的模.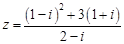 ,若
,若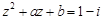 ,
,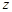 ;
;
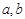 的值
的值