Question

已知

x≥1 x-y≤0 x2+y2-2x-6y+6≤0

，则x+2y的最大值为

7+2

5

．

Answer 1

分析：作出题中不等式组表示的平面区域，得到如图所示的阴影部分．再将直线l：z=x+2y进行平移并观察截距的变化，可得当l与区域相切于点A时达到x+2y的最大值．由此将圆x²+y²-2x-6y+6=0与直线方程联解得出A的坐标，代入目标函数即可求出x+2y的最大值．

解答：解：作出不等式组

x≥1 x-y≤0 x2+y2-2x-6y+6≤0

表示的平面区域，
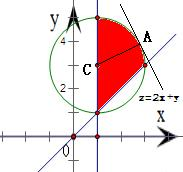
得到如图所示的阴影部分
将直线l：z=x+2y进行平移，可得当l与区域相切于点A时，
目标函数取得最大值
求得圆x²+y²-2x-6y+6=0的圆心C（1，3）
∵直线l与圆C相切，
∴CA⊥l，可得A（1+

2 5

5

，3+

4 5

5

）
因此，z=x+2y的最大值为z_max=1+

2 5

5

+2（3+

4 5

5

）=7+2

5

故答案为：7+2

5

点评：本题给出二元一次不等式组，求目标函数z=x+2y的最大值，着重考查了直线与圆的位置关系、二元不等式组表示的平面区域和简单的线性规划等知识，属于基础题．