题目内容
(12分)(理)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
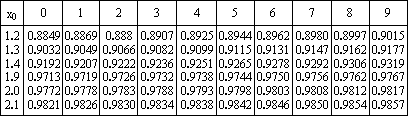
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?可共查阅的(部分)标准正态分布表
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
(理)解:(Ⅰ)设参赛学生的分数为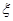 ,因为
,因为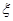 ~N(70,100),由条件知,
~N(70,100),由条件知,
P(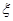 ≥90)=1-P(
≥90)=1-P(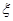 <90)=1-F(90)=1-
<90)=1-F(90)=1-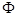
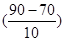 =1-
=1-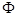 (2)=1-0.9772=0.228.
(2)=1-0.9772=0.228.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,因此,
参赛总人数约为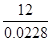 ≈526(人)。
≈526(人)。
(Ⅱ)假定设奖的分数线为x分,则
P(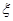 ≥x)=1-P(
≥x)=1-P(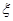 <x)=1-F(90)=1-
<x)=1-F(90)=1-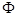
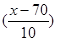 =
=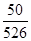 =0.0951,
=0.0951,
即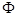
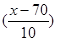 =0.9049,查表得
=0.9049,查表得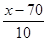 ≈1.31,解得x=83.1.
≈1.31,解得x=83.1.
故设奖得分数线约为83.1分。
【解析】略

(06年湖北卷理)(10分)
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布![]() 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表![]()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布![]() 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表![]()
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.2 1.3 1.4 1.9 2.0 2.1 | 0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 | 0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 | 0.888 0.9066 0.9222 0.9726 0.9783 0.9830 | 0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 | 0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 | 0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 | 0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 | 0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 | 0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 | 0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
点评:本小题主要考查正态分布,对独立事件的概念和标准正态分布的查阅,考查运用概率统计知识解决实际问题的能力。