题目内容
若点P(2,-1)为圆(x-1)2+y2=25的弦AB的中点,则直线AB的方程是 .
【答案】分析:求出圆心C的坐标,得到PC的斜率,利用中垂线的性质求得直线AB的斜率,点斜式写出AB的方程,并化为一般式.
解答:解:圆(x-1)2+y2=25的圆心C(1,0),点P(2,-1)为 弦AB的中点,PC的斜率为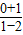 =-1,
=-1,
∴直线AB的斜率为1,点斜式写出直线AB的方程 y+1=1×(x-2),即 x-y-3=0,
故答案为 x-y-3=0.
点评:本题考查直线和圆相交的性质,线段的中垂线的性质,用点斜式求直线的方程的方法.
解答:解:圆(x-1)2+y2=25的圆心C(1,0),点P(2,-1)为 弦AB的中点,PC的斜率为
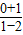 =-1,
=-1,∴直线AB的斜率为1,点斜式写出直线AB的方程 y+1=1×(x-2),即 x-y-3=0,
故答案为 x-y-3=0.
点评:本题考查直线和圆相交的性质,线段的中垂线的性质,用点斜式求直线的方程的方法.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目