题目内容
例3.已知奇函数f(x)在[2,4)上单调递减,试比较a=f(log| 1 |
| 2 |
| 3π |
| 4 |
分析:先根据f(x)为奇函数,分别求得a=-f(3),b=-f(π),再根据函数的单调性,得出结果.
解答:解:f(x)为奇函数
∴a=f(log
8)=f(-3)=-f(3),b=f(πtan
)=f(-π)=-f(π)
∵函数f(x)在[2,4)上单调递减,3<π
∴f(3)>f(π)
∴-f(3)<-f(π)
∴a<b
∴a=f(log
| 1 |
| 2 |
| 3π |
| 4 |
∵函数f(x)在[2,4)上单调递减,3<π
∴f(3)>f(π)
∴-f(3)<-f(π)
∴a<b
点评:本题主要考查函数的单调性和奇偶性的综合运用.属基础题.

练习册系列答案
相关题目
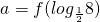 与
与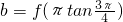 的大小.
的大小.