题目内容
a,b,c是△ABC的三边长,关于x的方程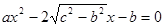 (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
(a>c>b)的两根之差的平方等于4,△ABC的面积S=10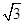 ,c=7.
,c=7.
(1)求角C;
(2)求a、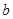 的值.
的值.
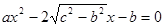 (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
(a>c>b)的两根之差的平方等于4,△ABC的面积S=10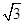 ,c=7.
,c=7.(1)求角C;
(2)求a、
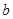 的值.
的值. (1) C=60°.(2)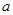 =8,
=8,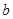 =5.
=5.
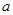 =8,
=8,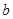 =5.
=5.(1)设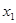 ,
,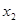 为方程
为方程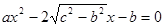 的两根,
的两根,
因为(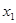 -
-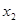 )2=(
)2=(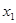 +
+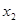 )2-4
)2-4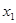
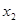 ,利用韦达定理可得
,利用韦达定理可得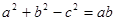 ,
,
从而借助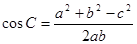 ,可得
,可得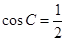 ,∴C=60°.
,∴C=60°.
(2)由S=
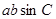 =10
=10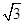 ,∴
,∴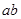 =40,再由
=40,再由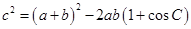 ,
,
从而可求a+b,然后再与ab=40解方程组可求出a,b的值.
(1)设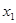 ,
,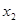 为方程
为方程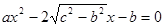 的两根,
的两根,
则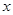 1+
1+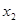 =
=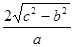 ,
,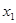 ·
·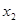 =-
=-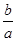 ,
,
∴(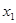 -
-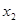 )2=(
)2=(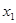 +
+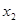 )2-4
)2-4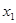
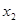 =
=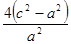 +
+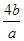 =4.∴
=4.∴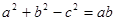
又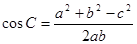 =
= ,∴C=60°.
,∴C=60°.
(2)由S=
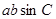 =10
=10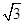 ,∴
,∴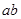 =40①
=40①
由余弦定理: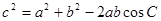 ,即
,即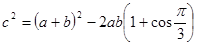
即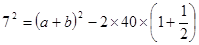 ∴
∴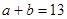 ②,由①②得:
②,由①②得: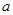 =8,
=8,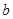 =5.
=5.
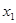 ,
,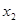 为方程
为方程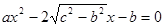 的两根,
的两根,因为(
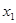 -
-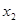 )2=(
)2=(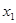 +
+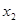 )2-4
)2-4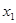
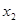 ,利用韦达定理可得
,利用韦达定理可得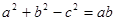 ,
,从而借助
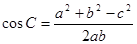 ,可得
,可得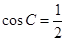 ,∴C=60°.
,∴C=60°.(2)由S=

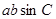 =10
=10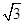 ,∴
,∴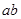 =40,再由
=40,再由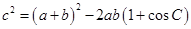 ,
,从而可求a+b,然后再与ab=40解方程组可求出a,b的值.
(1)设
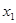 ,
,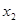 为方程
为方程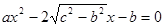 的两根,
的两根,则
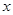 1+
1+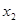 =
=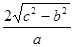 ,
,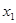 ·
·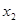 =-
=-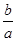 ,
,∴(
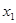 -
-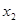 )2=(
)2=(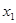 +
+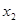 )2-4
)2-4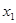
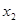 =
=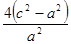 +
+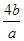 =4.∴
=4.∴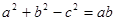
又
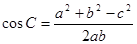 =
= ,∴C=60°.
,∴C=60°.(2)由S=

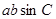 =10
=10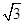 ,∴
,∴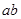 =40①
=40①由余弦定理:
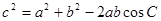 ,即
,即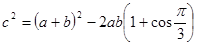
即
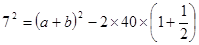 ∴
∴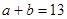 ②,由①②得:
②,由①②得: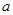 =8,
=8,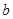 =5.
=5.
练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 中,设角
中,设角 的对边分别是
的对边分别是 ,
, ,
, .
. 的值;
的值; ,求
,求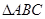 的内角A、B、C所对的边分别为
的内角A、B、C所对的边分别为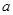 、b、c,已知
、b、c,已知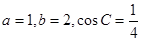
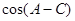 的值.
的值.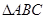 中,已知
中,已知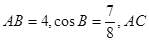 边上的中线
边上的中线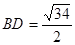 ,则
,则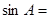 ( )
( )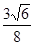
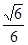
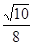
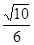
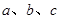
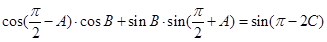 .
.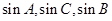 成等差数列,且
成等差数列,且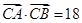 ,求边
,求边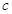 的长.
的长. ,则
,则 的最大值为 .
的最大值为 .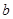 =2
=2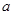 sin B,则角A为( )
sin B,则角A为( )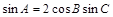 ,则△ABC的形状是( )
,则△ABC的形状是( )