题目内容
3.在△ABC中,M,N,P分别是AB,BC,CA边上靠近A,B,C的三等分点,O是△ABC平面上的任意一点,若$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\frac{1}{3}$$\overrightarrow{{e}_{1}}$-$\frac{1}{2}$$\overrightarrow{{e}_{2}}$,则$\overrightarrow{OM}$+$\overrightarrow{ON}$+$\overrightarrow{OP}$=$\frac{1}{3}\overrightarrow{{e}_{1}}$$-\frac{1}{2}\overrightarrow{{e}_{2}}$.分析 根据条件可得到BA=3MA,CB=3NB,AC=3PC,从而有$\overrightarrow{BA}=3\overrightarrow{MA}$,这样便可得到$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$,从而同理可得到$\overrightarrow{ON}=\frac{2}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$,$\overrightarrow{OP}=\frac{2}{3}\overrightarrow{OC}+\frac{1}{3}\overrightarrow{OA}$,这样进行向量的加法和数乘运算便可得出$\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}$.
解答 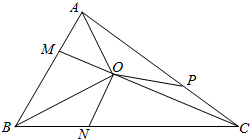 解:如图,M为AB的三等分点,且M靠近A;
解:如图,M为AB的三等分点,且M靠近A;
∴$\overrightarrow{BA}=3\overrightarrow{MA}$;
∴$\overrightarrow{OA}-\overrightarrow{OB}=3(\overrightarrow{OA}-\overrightarrow{OM})$;
∴$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;
同理,$\overrightarrow{ON}=\frac{2}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$,$\overrightarrow{OP}=\frac{2}{3}\overrightarrow{OC}+\frac{1}{3}\overrightarrow{OA}$;
∴$\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$=$\frac{1}{3}\overrightarrow{{e}_{1}}-\frac{1}{2}\overrightarrow{{e}_{2}}$.
故答案为:$\frac{1}{3}\overrightarrow{{e}_{1}}-\frac{1}{2}\overrightarrow{{e}_{2}}$.
点评 考查共线向量基本定理,向量减法、数乘的几何意义,以及向量的数乘运算.

 全能练考卷系列答案
全能练考卷系列答案