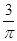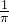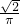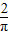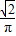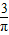题目内容
在半径为1的圆中随机地投一个点,则点落在圆内接正方形中的概率是( )
分析:根据题意,设圆的圆心为O,其内接正方形为ABCD,由圆的半径,可得圆的面积,连接OA、OB,易得△AOB为等腰直角三角形,由勾股定理,可得AB的长,进而可得正方形为ABCD的面积,由几何概型公式,计算可得答案.
解答: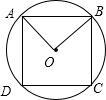 解:根据题意,设圆的圆心为O,其内接正方形为ABCD,连接OA、OB,
解:根据题意,设圆的圆心为O,其内接正方形为ABCD,连接OA、OB,
圆O的半径为1,则其面积为π•12=π,
易得△AOB为等腰直角三角形,且∠AOB=90°,OA=OB=1;
AB=
=
,
S□ABCD=2,
则点落在圆内接正方形中的概率P=
,
故选B.
 解:根据题意,设圆的圆心为O,其内接正方形为ABCD,连接OA、OB,
解:根据题意,设圆的圆心为O,其内接正方形为ABCD,连接OA、OB,圆O的半径为1,则其面积为π•12=π,
易得△AOB为等腰直角三角形,且∠AOB=90°,OA=OB=1;
AB=
| 12+12 |
| 2 |
S□ABCD=2,
则点落在圆内接正方形中的概率P=
| 2 |
| π |
故选B.
点评:本题考查几何概型的计算,关键是求出圆内接正方形的边长,进而求出其面积.

练习册系列答案
相关题目
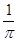 B、
B、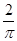 C、
C、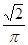 D 、
D 、