题目内容
下列说法:
①x>2是x2-3x+2>0的充分不必要条件.
②函数y=
图象的对称中心是(1,1).
③已知x,y∈R,i为虚数单位,且(x-2)i-y=1+i,则(1+i)x-y的值为-4.
④若函数f(x)=
,对任意的x1≠x2都有
<0,则实数a的取值范围是(
,1).
其中正确命题的序号为
①x>2是x2-3x+2>0的充分不必要条件.
②函数y=
| x-1 |
| x+1 |
③已知x,y∈R,i为虚数单位,且(x-2)i-y=1+i,则(1+i)x-y的值为-4.
④若函数f(x)=
|
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 7 |
其中正确命题的序号为
①③
①③
.分析:x>2⇒x2-3x+2>0,x2-3x+2>0⇒x>2或x<1,故x>2是x2-3x+2>0的充分不必要条件;由函数y=
=1-
,知函数y=
图象的对称中心是(-1,1);由(x-2)i-y=1+i,知
,故(1+i)x-y=(1+i)4=(2i)2=-4;由对任意的x1≠x2都有
<0,知函数f(x)=
是减函数,由此能求出0<a<
.
| x-1 |
| x+1 |
| 2 |
| x+1 |
| x-1 |
| x+1 |
|
| f(x2)-f(x1) |
| x2-x1 |
|
| 1 |
| 3 |
解答:解:x>2⇒x2-3x+2>0,
x2-3x+2>0⇒x>2或x<1,
∴x>2是x2-3x+2>0的充分不必要条件,故①是真命题;
∵函数y=
=1-
,
∴函数y=
图象的对称中心是(-1,1),故②是假命题;
∵(x-2)i-y=1+i,
∴
,即x=3,y=-1,
∴(1+i)x-y=(1+i)4=(2i)2=-4,即③是真命题;
∵对任意的x1≠x2都有
<0,
∴函数f(x)=
是减函数,
∴
,即0<a<
,故④是假命题.
故答案为:①③.
x2-3x+2>0⇒x>2或x<1,
∴x>2是x2-3x+2>0的充分不必要条件,故①是真命题;
∵函数y=
| x-1 |
| x+1 |
| 2 |
| x+1 |
∴函数y=
| x-1 |
| x+1 |
∵(x-2)i-y=1+i,
∴
|
∴(1+i)x-y=(1+i)4=(2i)2=-4,即③是真命题;
∵对任意的x1≠x2都有
| f(x2)-f(x1) |
| x2-x1 |
∴函数f(x)=
|
∴
|
| 1 |
| 3 |
故答案为:①③.
点评:本题考查命题的真假判断,是基础题.解题时要注意不等式、函数的对称性、复数性质、对数函数等知识点的灵活运用.

练习册系列答案
相关题目
 图象的对称中心是(1,1).
图象的对称中心是(1,1). ,对任意的x1≠x2都有
,对任意的x1≠x2都有 ,则实数a的取值范围是
,则实数a的取值范围是 .
. 图象的对称中心是(1,1).
图象的对称中心是(1,1). ,对任意的x1≠x2都有
,对任意的x1≠x2都有 ,则实数a的取值范围是
,则实数a的取值范围是 .
. 图象的对称中心是(1,1).
图象的对称中心是(1,1). ,对任意的x1≠x2都有
,对任意的x1≠x2都有 ,则实数a的取值范围是
,则实数a的取值范围是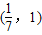 .
.