题目内容
已知函数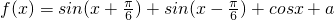 的最大值为1.
的最大值为1.
(1)求常数a的值;
(2)求f(x)的单调增区间.
必修四P147例12改编
解:(1)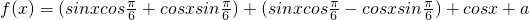 (4分)
(4分)
=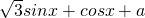 =
=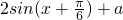 (6分)
(6分)
∴f(x)max=2+a=1,∴a=-1.(8分)
(2)由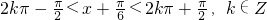 (10分)
(10分)
得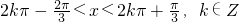
所以f(x)的单调增区间为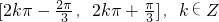 . (12分)
. (12分)
分析:(1)利用两角和与差的三角函数化简函数的表达式,通过函数的最大值即可求出a的值.
直接利用正弦函数的单调增区间求出函数的单调增区间即可.
点评:本题考查正弦函数的单调性,两角和与差的正弦函数,正弦函数的定义域和值域,考查基本知识的灵活运用.
解:(1)
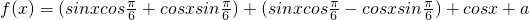 (4分)
(4分)=
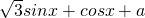 =
=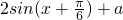 (6分)
(6分)∴f(x)max=2+a=1,∴a=-1.(8分)
(2)由
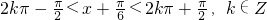 (10分)
(10分)得
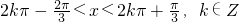
所以f(x)的单调增区间为
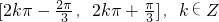 . (12分)
. (12分)分析:(1)利用两角和与差的三角函数化简函数的表达式,通过函数的最大值即可求出a的值.
直接利用正弦函数的单调增区间求出函数的单调增区间即可.
点评:本题考查正弦函数的单调性,两角和与差的正弦函数,正弦函数的定义域和值域,考查基本知识的灵活运用.

练习册系列答案
相关题目
 的最大值为1.
的最大值为1. 的最大值为1.
的最大值为1. 的值;(2)求使
的值;(2)求使 成立的x的取值集合.
成立的x的取值集合. 的最大值为1,最小值为
的最大值为1,最小值为 ,则函数
,则函数 的最大值为
的最大值为  的最大值为
的最大值为 .
. 的值;
的值; 成立的
成立的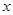 的取值范围.
的取值范围.