Question

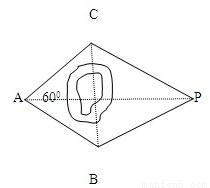
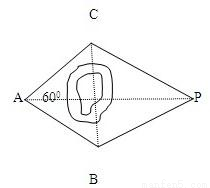
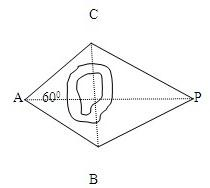某大队在农田基本建设的规划中，要测定被障碍物隔开的两点A和P之间的距离，他们土法上马，在障碍物的两侧，选取两点B和C（如图），测得AB=AC=50 m，∠BAC=60°，∠ABP=120°，∠ACP=135°，求A和P之间的距离（答案可用最简根式表示）．

Answer 1

分析：连CB，AP根据∠CAB=60°和AC=AB判定△ABC为等边三角形．进而可求得∠BCP，∠CBP和∠BPC，再通过正弦定理进而可求得CP，再在△APC中用余弦定理求得AP．

解答：解：连CB，AP．
∵∠CAB=60°，
AC=AB=50m，
∴△ABC为等边三角形．
于是，∠BCP=135°-60°=75°，
∠CBP=120°-60°，
∠BPC=180°-（75°+60°）=45°
由正弦定理，得

CP

sin∠CBP

=

CB

sin∠BPC

CP=

CB•sin∠CBP

sin∠BPC

=

50•sin60°

sin45°

=

50• 3 2

2 2

=25

6

(m)
由余弦定理，可得AP²=AC²+CP²-2•AC•CP•cos135°
=502+(25

6

)2-2•50•25

6

•(-

2

2

)
=625(10+4

3

)(m2)
AP=

625(10+4 3 )

=25

10+4 3

（m）
故A、P两点间的距离是25

10+4 3

米．

点评：本题主要考查正弦定理和余弦定理在实际中的应用．属基础题．