题目内容
探究函数f(x)= 的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.
的最小值,并确定取得最小值时x的值.列表如下,请观察表中y值随x值变化的特点,完成以下的问题.| x | … | 0.25 | 0.5 | 0.75 | 1 | 1.1 | 1.2 | 1.5 | 2 | 3 | 5 | … |
| y | … | 8.063 | 4.25 | 3.229 | 3 | 3.028 | 3.081 | 3.583 | 5 | 9.667 | 25.4 | … |
 在区间(0,1)上递减,问:
在区间(0,1)上递减,问:(1)函数f(x)=
 在区间______上递增.当x=______时,y最小=______;
在区间______上递增.当x=______时,y最小=______;(2)函数
 在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
在定义域内有最大值或最小值吗?如有,是多少?此时x为何值?(直接回答结果,不需证明)
【答案】分析:(1)由表中数据可推测函数f(x)在区间[1,+∞)上递增,从而当x=1 时,y最小=3,证明此结论可利用导数或均值定理;
(2)利用换元法,设t=|3x|,将函数g(x)转化为函数f(t),利用(1)中的结论求最值即可
解答:解:(1)由表中数据可知:函数f(x)= 在区间[1,+∞)上递增.
在区间[1,+∞)上递增.
当x=1 时,y最小=3.
故答案为[1,+∞),1,3
(2)由函数g(x)=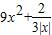 =(3x)2+
=(3x)2+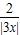 =t2+
=t2+ ,(令t=|3x|),
,(令t=|3x|),
由(1)知函数g(x)有最小值3,
又因为g(-x)=g(x),所以g(x)是偶函数,
所以函数g(x)取得最小值时t=3|x|=1,即x=±
点评:本题主要考查了利用列表法研究函数性质的方法,利用换元法求函数最值的方法,转化化归的思想方法
(2)利用换元法,设t=|3x|,将函数g(x)转化为函数f(t),利用(1)中的结论求最值即可
解答:解:(1)由表中数据可知:函数f(x)=
 在区间[1,+∞)上递增.
在区间[1,+∞)上递增.当x=1 时,y最小=3.
故答案为[1,+∞),1,3
(2)由函数g(x)=
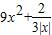 =(3x)2+
=(3x)2+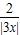 =t2+
=t2+ ,(令t=|3x|),
,(令t=|3x|),由(1)知函数g(x)有最小值3,
又因为g(-x)=g(x),所以g(x)是偶函数,
所以函数g(x)取得最小值时t=3|x|=1,即x=±

点评:本题主要考查了利用列表法研究函数性质的方法,利用换元法求函数最值的方法,转化化归的思想方法

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目