题目内容
M是椭圆 上的任意一点,F1、F2是椭圆的左、右焦点,则|MF1|•|MF2|的最大值是________.
上的任意一点,F1、F2是椭圆的左、右焦点,则|MF1|•|MF2|的最大值是________.
9
分析:由题意可设M(x0,y0),可先求出离心率,然后根据椭圆的第二定义用x0分别表示出|MF1|和|MF2|,求出|MF1|•|MF2|的表达式,把其看为关于x0的二次函数,利用二次函数的性质求出其最大值.
解答:设M(x0,y0),由题意知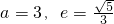 ,
,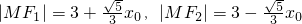 ,
,
∴|MF1|•|MF2|=(3+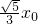 )(3-
)(3-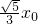 )=9-
)=9-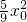 .
.
∴当x0=0时,|MF1|•|MF2|有最大值9.
故答案为:9.
点评:本题考查椭圆的性质和应用,解题时要认真审题,仔细解答.
分析:由题意可设M(x0,y0),可先求出离心率,然后根据椭圆的第二定义用x0分别表示出|MF1|和|MF2|,求出|MF1|•|MF2|的表达式,把其看为关于x0的二次函数,利用二次函数的性质求出其最大值.
解答:设M(x0,y0),由题意知
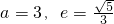 ,
,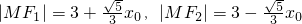 ,
,∴|MF1|•|MF2|=(3+
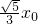 )(3-
)(3-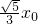 )=9-
)=9-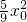 .
.∴当x0=0时,|MF1|•|MF2|有最大值9.
故答案为:9.
点评:本题考查椭圆的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 的左、右焦点分别为F1、F2,点M是椭圆上的任意一点,且|PF1|+|PF2|=4,椭圆的离心率
的左、右焦点分别为F1、F2,点M是椭圆上的任意一点,且|PF1|+|PF2|=4,椭圆的离心率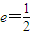 .
.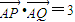 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.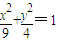 上的任意一点,F1、F2是椭圆的左、右焦点,则|MF1|•|MF2|的最大值是 .
上的任意一点,F1、F2是椭圆的左、右焦点,则|MF1|•|MF2|的最大值是 .