题目内容
张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润x(元)与年产量t(吨)满足函数关系 .若工厂每生产一吨产品必须赔付农场s元(以下称s为赔付价格).
.若工厂每生产一吨产品必须赔付农场s元(以下称s为赔付价格).
(1)将工厂的年利润w(元)表示为年产量t(吨)的函数,并求出工厂获得最大利润的年产量;
(2)若农场每年受工厂生产影响的经济损失金额y=0.002t2(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格s是多少?
解:(Ⅰ)工厂的实际年利润为: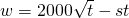 (t≥0).
(t≥0).
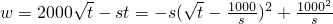 ,
,
当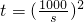 时,w取得最大值.
时,w取得最大值.
所以工厂取得最大年利润的年产量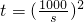 (吨).
(吨).
(Ⅱ)设农场净收入为v元,则v=st-0.002t2.
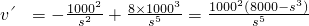 ,
,
将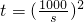 代入上式,
代入上式,
得: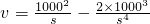 .
.
又令v'=0,得s=20. 当s<20时,v'>0;当s>20时,v'<0,
所以当s=20时,v取得最大值.
故在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格s为20元.
分析:(1)由已知中赔付价格为s元/吨,所以工厂的实际年利润为w=2000 -st.我们利用配方法易求出工厂方取得最大年利润的年产量;
-st.我们利用配方法易求出工厂方取得最大年利润的年产量;
(2)由已知得,若农场净收入为v元,则v=st-0.002t2.再由x=2000 .我们可以得到农场净收入v与赔付价格s之间的函数关系式,利用导数法,我们易求出答案.
.我们可以得到农场净收入v与赔付价格s之间的函数关系式,利用导数法,我们易求出答案.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.
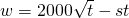 (t≥0).
(t≥0).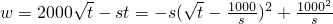 ,
,当
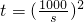 时,w取得最大值.
时,w取得最大值.所以工厂取得最大年利润的年产量
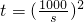 (吨).
(吨).(Ⅱ)设农场净收入为v元,则v=st-0.002t2.
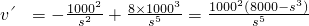 ,
,将
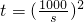 代入上式,
代入上式,得:
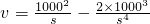 .
.又令v'=0,得s=20. 当s<20时,v'>0;当s>20时,v'<0,
所以当s=20时,v取得最大值.
故在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格s为20元.
分析:(1)由已知中赔付价格为s元/吨,所以工厂的实际年利润为w=2000
 -st.我们利用配方法易求出工厂方取得最大年利润的年产量;
-st.我们利用配方法易求出工厂方取得最大年利润的年产量;(2)由已知得,若农场净收入为v元,则v=st-0.002t2.再由x=2000
 .我们可以得到农场净收入v与赔付价格s之间的函数关系式,利用导数法,我们易求出答案.
.我们可以得到农场净收入v与赔付价格s之间的函数关系式,利用导数法,我们易求出答案.点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
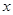 (元)与年产量
(元)与年产量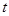 (吨)满足函数关系
(吨)满足函数关系 .若工厂每生产一吨产品必须赔付农场
.若工厂每生产一吨产品必须赔付农场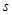 元(以下称
元(以下称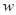 (元)表示为年产量
(元)表示为年产量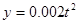 (元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格
(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格