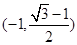题目内容
函数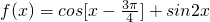 的值域是
的值域是
- A.[-2,0]
- B.[-2,
 ]
] - C.[-1,1]
- D.
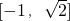
B
分析:利用三角函数的恒等变换化简函数f(x)的解析式为 (sinx-cosx)+2sinxcosx,设
(sinx-cosx)+2sinxcosx,设  (sinx-cosx)=t,则 f(x)=-2t2+t+1,t∈[-1,1].再利用二次函数的性质,求出函数的最大值和最小值,从而求得函数的值域.
(sinx-cosx)=t,则 f(x)=-2t2+t+1,t∈[-1,1].再利用二次函数的性质,求出函数的最大值和最小值,从而求得函数的值域.
解答:∵函数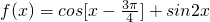 =-
=- cosx+
cosx+ sinx+sin2x=
sinx+sin2x= (sinx-cosx)+2sinxcosx,
(sinx-cosx)+2sinxcosx,
设 (sinx-cosx)=t,平方可得 2sinxcosx=1-2t2,且-1≤t≤1,∴f(x)=-2t2+t+1,t∈[-1,1].
(sinx-cosx)=t,平方可得 2sinxcosx=1-2t2,且-1≤t≤1,∴f(x)=-2t2+t+1,t∈[-1,1].
故当t= 时,函数f(x)=-2t2+t+1取得最大值为
时,函数f(x)=-2t2+t+1取得最大值为 ,当t=-1时,函数f(x)=-2t2+t+1取得最小值为-2,
,当t=-1时,函数f(x)=-2t2+t+1取得最小值为-2,
故函数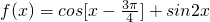 的值域是[-2,
的值域是[-2, ].
].
点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,二次函数的性质应用,属于中档题.
分析:利用三角函数的恒等变换化简函数f(x)的解析式为
 (sinx-cosx)+2sinxcosx,设
(sinx-cosx)+2sinxcosx,设  (sinx-cosx)=t,则 f(x)=-2t2+t+1,t∈[-1,1].再利用二次函数的性质,求出函数的最大值和最小值,从而求得函数的值域.
(sinx-cosx)=t,则 f(x)=-2t2+t+1,t∈[-1,1].再利用二次函数的性质,求出函数的最大值和最小值,从而求得函数的值域.解答:∵函数
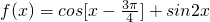 =-
=- cosx+
cosx+ sinx+sin2x=
sinx+sin2x= (sinx-cosx)+2sinxcosx,
(sinx-cosx)+2sinxcosx,设
 (sinx-cosx)=t,平方可得 2sinxcosx=1-2t2,且-1≤t≤1,∴f(x)=-2t2+t+1,t∈[-1,1].
(sinx-cosx)=t,平方可得 2sinxcosx=1-2t2,且-1≤t≤1,∴f(x)=-2t2+t+1,t∈[-1,1].故当t=
 时,函数f(x)=-2t2+t+1取得最大值为
时,函数f(x)=-2t2+t+1取得最大值为 ,当t=-1时,函数f(x)=-2t2+t+1取得最小值为-2,
,当t=-1时,函数f(x)=-2t2+t+1取得最小值为-2,故函数
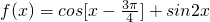 的值域是[-2,
的值域是[-2, ].
].点评:本题主要考查三角函数的恒等变换及化简求值,复合三角函数的单调性,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
 ,则函数
,则函数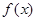 的值域是( ).
的值域是( ).  B.
B.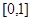 C.
C.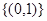 D.
D.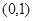
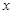 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数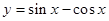 的值域是( )
的值域是( ) B.
B.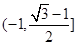 C.
C.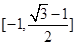 D.
D.