题目内容
已知 ,且关于
,且关于 的函数
的函数 在
在 上有极值,则
上有极值,则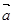 与
与 的夹角范围( )
的夹角范围( )
A. | B. | C. | D. |
C
解析试题分析:函数 在
在 上有极值,即
上有极值,即 对应的方程有解,所以
对应的方程有解,所以 ,又因为
,又因为 ,所以
,所以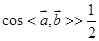 ,所以
,所以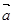 与
与 的夹角范围为
的夹角范围为 .
.
考点:本小题主要考查函数的极值,向量的夹角.
点评:解决本小题时要注意两个向量的夹角的取值范围.

练习册系列答案
相关题目
设 、
、 都是非零向量,下列四个条件中,一定能使
都是非零向量,下列四个条件中,一定能使 成立的是( )
成立的是( )
A. | B. | C. | D. |
已知O是△ABC内一点,若 ,则△AOC与△ABC的面积的比值为 ( )
,则△AOC与△ABC的面积的比值为 ( )
A. | B. | C. | D. |
已知点G是ΔABC的重心, ,
,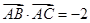 ,则
,则 的最小值是
的最小值是
A.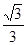 | B. | C. | D. |
已知平面向量 ,
, ,则
,则
| A.-10 | B.10 | C.-20 | D.20 |
已知O是坐标原点, ,若点
,若点 为平面区域
为平面区域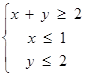 上一动点,则
上一动点,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
△ 内接于以
内接于以 为圆心,1为半径的圆,且
为圆心,1为半径的圆,且 则
则 .
. 的值为( )
的值为( )
A. | B.  | C. | D. |
设点P是△ABC所在平面内一点, ,则点P是△ABC
,则点P是△ABC
| A.内心 | B.外心 | C.重心 | D.垂心 |
 、
、 是非零向量,它们之间有如下一种运算:
是非零向量,它们之间有如下一种运算: ,其中
,其中 表示
表示 ;
; ;
; ;
; ;
; ,
, ,则
,则 .
.