题目内容
设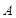 是同时符合以下性质的函数
是同时符合以下性质的函数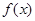 组成的集合:
组成的集合:
①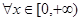 ,都有
,都有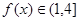 ;②
;②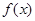 在
在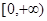 上是减函数.
上是减函数.
(1)判断函数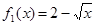 和
和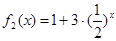 (
(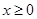 )是否属于集合
)是否属于集合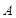 ,并简要说明理由;
,并简要说明理由;
(2)把(1)中你认为是集合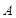 中的一个函数记为
中的一个函数记为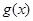 ,若不等式
,若不等式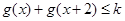 对任意的
对任意的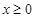 总成立,求实数
总成立,求实数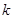 的取值范围.
的取值范围.
【答案】
(1)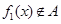 ,
, ;(2)
;(2)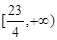 .
.
【解析】
试题分析:(1)对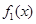 和
和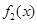 分别判断其单调性,然后再求出其值域即可得到答案;(2)
分别判断其单调性,然后再求出其值域即可得到答案;(2)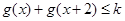 对任意的
对任意的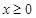 总成立,则可得
总成立,则可得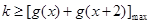 ,问题转化为求函数
,问题转化为求函数 的最大值,通过判断其单调性即可得到最大值.
的最大值,通过判断其单调性即可得到最大值.
试题解析:(1)∵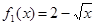 在
在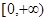 时是减函数,
时是减函数,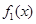 的值域为
的值域为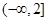 ,
,
∴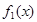 不在集合
不在集合 中
3分
中
3分
又∵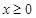 时,
时,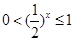 ,
,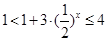 ,∴
,∴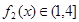 ,
5分
,
5分
且 在
在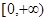 上是减函数,
上是减函数,
∴ 在集合
在集合 中
7分
中
7分
(2)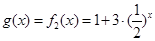 ,
,
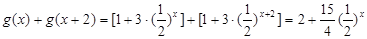 , 9分
, 9分
在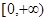 上是减函数,
上是减函数,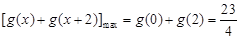 ,
11分
,
11分
又由已知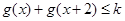 对任意的
对任意的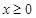 总成立,
总成立,
∴ ,因此所求的实数
,因此所求的实数 的取值范围是
的取值范围是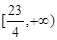 16分
16分
考点:函数的单调性、值域,不等式恒成立问题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 是同时符合以下性质的函数
是同时符合以下性质的函数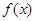 组成的集合:
组成的集合: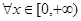 ,都有
,都有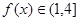 ;②
;②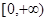 上是减函数.
上是减函数.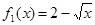 和
和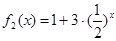 (
(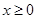 )是否属于集合
)是否属于集合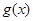 ,若不等式
,若不等式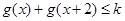 对任意的
对任意的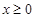 总成立,求实数
总成立,求实数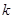 的取值范围.
的取值范围.