题目内容
有三颗骰子A、B、C,A的表面分别刻有1,2,3,4,5,6,B的表面分别刻有1,3,5,7,9,11,C的表面分别刻有2,4,6,8,10,12.(1)求抛掷A、B两颗骰子后向上的点数之和为奇数的概率?
(2)求抛掷三颗骰子后向上的点数之和为12的概率?
【答案】分析:(1)由题设条件,的结果是一个骰子出现奇数一个骰子出现偶数,由此易得出此事件包含的基本事件数,总的基本事件数为6×6=36,由次易求得此事件的概率;
(2)易求得,总的基本事件数为6×6×6=216,由于事件“抛掷三颗骰子后向上的点数之和为12”较复杂,故可采用列举法列举出所有的基本事件得出此事件包含的基本事件数,再由公式求出概率
解答:解:(1)抛掷A、B两颗骰子,总的基本事件数有6×6=36个
事件“抛掷A、B两颗骰子后向上的点数之和为奇数”只能是A骰子出现的点数是偶数,B骰子出现的点数是奇数,故此事件包含的基本事件数3×6=18
此事件发生的概率是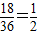 ,
,
即抛掷A、B两颗骰子后向上的点数之和为奇数的概率为
(2)抛掷三颗骰子,总的基本事件数6×6×6=216
由于事件“抛掷三颗骰子后向上的点数之和为12”情况较复杂,宜用列举法列举出基本事件的个数,基本事件有:
(1,1,10),(1,3,8),(1,5,6),(1,7,4),(1,9,2),(3,1,8),(3,3,6),(3,5,4),(3,7,2),(5,1,6),(5,3,4),(5,5,2),共12个
故事件“抛掷三颗骰子后向上的点数之和为12”的概率是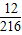 =
=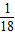
点评:本题考查等可能事件的概率,解题的关键是理解两个事件,根据两个事件的特征选择出恰当的计数方法,如本题中第二小题,根据所研究的事件比较复杂,采用了列举法计数.
(2)易求得,总的基本事件数为6×6×6=216,由于事件“抛掷三颗骰子后向上的点数之和为12”较复杂,故可采用列举法列举出所有的基本事件得出此事件包含的基本事件数,再由公式求出概率
解答:解:(1)抛掷A、B两颗骰子,总的基本事件数有6×6=36个
事件“抛掷A、B两颗骰子后向上的点数之和为奇数”只能是A骰子出现的点数是偶数,B骰子出现的点数是奇数,故此事件包含的基本事件数3×6=18
此事件发生的概率是
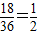 ,
,即抛掷A、B两颗骰子后向上的点数之和为奇数的概率为

(2)抛掷三颗骰子,总的基本事件数6×6×6=216
由于事件“抛掷三颗骰子后向上的点数之和为12”情况较复杂,宜用列举法列举出基本事件的个数,基本事件有:
(1,1,10),(1,3,8),(1,5,6),(1,7,4),(1,9,2),(3,1,8),(3,3,6),(3,5,4),(3,7,2),(5,1,6),(5,3,4),(5,5,2),共12个
故事件“抛掷三颗骰子后向上的点数之和为12”的概率是
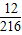 =
=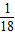
点评:本题考查等可能事件的概率,解题的关键是理解两个事件,根据两个事件的特征选择出恰当的计数方法,如本题中第二小题,根据所研究的事件比较复杂,采用了列举法计数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目