题目内容
5.存在函数f(x)满足,对任意x∈R都有( )| A. | f(sin2x)=sinx | B. | f(sin2x)=x2+x | C. | f(x2+1)=|x+1| | D. | f(x2+2x)=|x+1| |
分析 利用x取特殊值,通过函数的定义判断正误即可.
解答 解:A.取x=0,则sin2x=0,∴f(0)=0;
取x=$\frac{π}{2}$,则sin2x=0,∴f(0)=1;
∴f(0)=0,和1,不符合函数的定义;
∴不存在函数f(x),对任意x∈R都有f(sin2x)=sinx;
B.取x=0,则f(0)=0;
取x=π,则f(0)=π2+π;
∴f(0)有两个值,不符合函数的定义;
∴该选项错误;
C.取x=1,则f(2)=2,取x=-1,则f(2)=0;
这样f(2)有两个值,不符合函数的定义;
∴该选项错误;
D.令x+1=t,则f(x2+2x)=|x+1|,化为f(t2-1)=|t|;
令t2-1=x,则t=±$\sqrt{x+1}$;
∴$f(x)=\sqrt{x+1}$;
即存在函数f(x)=$\sqrt{x+1}$,对任意x∈R,都有f(x2+2x)=|x+1|;
∴该选项正确.
故选:D.
点评 本题考查函数的定义的应用,基本知识的考查,但是思考问题解决问题的方法比较难.

练习册系列答案
相关题目
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点到其渐近线的距离等于4,抛物线y2=2px的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为8,则抛物线方程为( )
| A. | y2=4x | B. | y2=4$\sqrt{2}x$ | C. | y2=8$\sqrt{2}x$ | D. | y2=16$\sqrt{2}x$ |
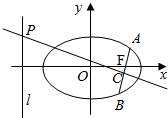 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,且右焦点F到左准线l的距离为3.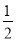 ,
,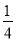 ,
,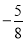 ,
,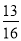 ,
,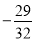 ,
,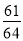 ,…
,…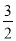 ,1,
,1,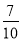 ,
,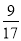 ,…
,… ,
, .
. 的解集为
的解集为 ,求
,求 的值;
的值; ,使
,使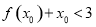 ,求
,求 的取值范围.
的取值范围.