题目内容
命题 :实数
:实数 满足
满足 ,其中
,其中 ,命题
,命题 :实数
:实数 满足
满足  或
或 ,且
,且  是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
-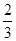 ≤a<0或a≤-4.
≤a<0或a≤-4.
解析试题分析:先对集合进行化简,由 是p的必要不充分条件,可知
是p的必要不充分条件,可知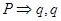 推不出p,所以
推不出p,所以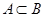 可得不等式
可得不等式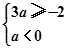 或
或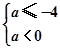 ,解不等式组即可.
,解不等式组即可.
试题解析:解:设A={x|x2-4ax+3a2<0(a<0)}={x|3a<x<a}, 2分
B={x|x2-x-6≤0或x2+2x-8<0}
={x|x2-x-6<0}∪{x|x2+2x-8>0}
={x|-2≤x≤3}∪{x|x<-4或x>2}={x|x<-4或x≥-2}. 4分
因为  是p的必要不充分条件,
是p的必要不充分条件,
所以 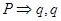 推不出p,由
推不出p,由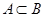 得 6分
得 6分
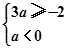 或
或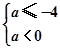 10分
10分
即-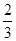 ≤a<0或a≤-4. 12分
≤a<0或a≤-4. 12分
考点:本题考查充要条件,集合之间的关系和运算.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

 ,求实数m的值;
,求实数m的值; ,求实数m的取值范围。
,求实数m的取值范围。 (其中
(其中 ).
). 时,求不等式的解集;
时,求不等式的解集; 的取值范围
的取值范围 是它的子集,
是它的子集, ;②若
;②若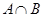 =B,求
=B,求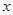 的值;③若
的值;③若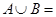
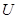 ,求
,求 ,求实数a的取值范围.
,求实数a的取值范围.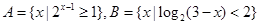 ,求
,求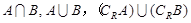 .
.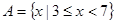 ,
,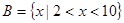 ,
,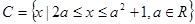 。
。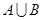 ,
,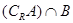 ;
;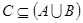 ,求实数
,求实数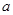 的取值范围.
的取值范围.  ,
, ,若
,若 Æ.则实数
Æ.则实数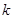 的取值范围是 .
的取值范围是 .