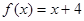题目内容
设![]() 是定义在
是定义在![]() 上以2为周期的函数,对
上以2为周期的函数,对![]() ,用
,用![]() 表示区间
表示区间![]() .
.
已知当![]() 时,函数
时,函数![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)对自然数![]() ,求集合
,求集合![]() {
{![]() 使方程
使方程![]() 在
在![]() 上有两个不相等的实根}
上有两个不相等的实根}
(1)![]()
(2)[1] 当![]() 时,
时, ![]()
![]() 或
或![]()
![]() ;
;
[2] 当![]() 时,
时, ![]()
![]()
![]() ;
;
[3] 当![]() 时,
时, ![]()
![]()
![]()
解析:
(1)因为![]() 是以2为周期的函数,所以当
是以2为周期的函数,所以当![]() 时,
时,![]() 是
是![]() 的周期函数
的周期函数
又当![]() 时,
时,![]() ,所以
,所以![]() ,
,
 即当
即当![]() ,
,![]() 时,
时,![]() . ………………3分;
. ………………3分;
(2)[1] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
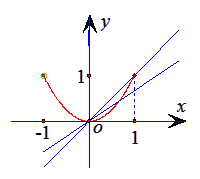
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]() 或
或![]()
![]() 即可………5分
即可………5分
 [2] 当
[2] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
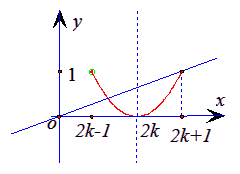
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]()
![]() 即可……….7分
即可……….7分
 [3] 当
[3] 当![]() 时,
时, ![]() 表示区间
表示区间![]() , 此时
, 此时![]() , 令
, 令![]() 则欲使方程
则欲使方程![]() 有两个不等根,即使
有两个不等根,即使![]() 与
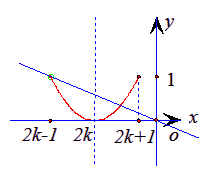
与![]() 这两个函数图像有两个不同交点.如图所示,
这两个函数图像有两个不同交点.如图所示,
只要:![]()
![]()
![]() 即可……………9分
即可……………9分
综上所述:[1] 当![]() 时,
时, ![]()
![]() 或
或![]()
![]() ;
;
[2] 当![]() 时,
时, ![]()
![]()
![]() ;
;
[3] 当![]() 时,
时, ![]()
![]()
![]() ……………10分
……………10分
注: 本题还可以用“根的分布”的方法,请酌情给分.

练习册系列答案
相关题目
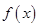 是定义在
是定义在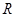 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知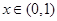 ,
,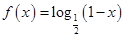 ,则函数
,则函数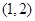 上的解析式是
上的解析式是 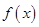 是定义在
是定义在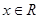 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知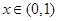 ,
,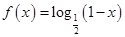 ,则函数
,则函数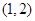 上( )
上( )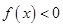 B.是增函数且
B.是增函数且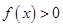
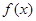 是定义在
是定义在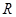 上以2为周期的偶函数,当
上以2为周期的偶函数,当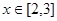 时,
时,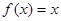 则
则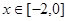 时
时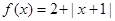 B.
B.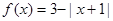
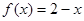 D.
D.