题目内容
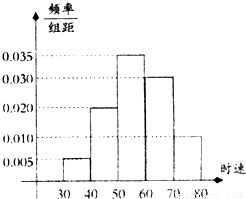
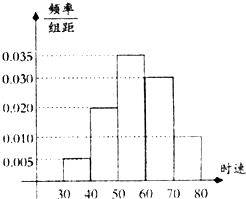 在一段时间内有100辆汽车经过某交通岗,时速(单位:km/h)频率分布直方图如图所示,
在一段时间内有100辆汽车经过某交通岗,时速(单位:km/h)频率分布直方图如图所示,(1)求时速超过60km/h的汽车的数量;
(2)从时速在[30,40)与[70,80]的两部分中共取两辆汽车,速度分别为v1,v2,求这两辆汽车的时速满足|v1-v2|≤10的概率.
(3)以在这段时间内经过交通岗的汽车的频率为概率,求在此交通岗经过的5辆汽车中恰有2辆汽车的速度在[40,50)的概率.
分析:(1)利用频率直方图先求出时速超过60km/h的两个矩形的面积,然后确定汽车数量.
(2)结合频率直方图求出时速在[30,40)与[70,80]的车辆数,然后利用古典概型求满足条件的概率.
(3)利用独立事件同时发生的概率公式求在此交通岗经过的5辆汽车中恰有2辆汽车的速度在[40,50)的概率.
(2)结合频率直方图求出时速在[30,40)与[70,80]的车辆数,然后利用古典概型求满足条件的概率.
(3)利用独立事件同时发生的概率公式求在此交通岗经过的5辆汽车中恰有2辆汽车的速度在[40,50)的概率.
解答:解:(1)时速超过60km/h的汽车的数量为(0.03+0.01)×10×100=40(辆);
(2)记两辆汽车的时速满足|v1-v2|≤10为事件A;
又两辆汽车的时速满足|v1-v2|≤10,
即:在[30,40)中共取两辆汽车或在[70,80]中共取两辆汽车,
而[30,40)中有5辆车,[70,80]中有10辆车;
则:P(A)=
=
;
(3)记此交通岗经过的5辆汽车中恰有2辆汽车的速度在[40,50)为事件B,又在这段时间内经过交通岗的汽车速度在[40,50)的概率为
,则P(B)=
(
)2(
)3=
;
(2)记两辆汽车的时速满足|v1-v2|≤10为事件A;
又两辆汽车的时速满足|v1-v2|≤10,
即:在[30,40)中共取两辆汽车或在[70,80]中共取两辆汽车,
而[30,40)中有5辆车,[70,80]中有10辆车;
则:P(A)=
| ||||
|
| 11 |
| 12 |
(3)记此交通岗经过的5辆汽车中恰有2辆汽车的速度在[40,50)为事件B,又在这段时间内经过交通岗的汽车速度在[40,50)的概率为
| 1 |
| 5 |
| C | 2 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 128 |
| 625 |
点评:本题考查频率分布直方图的相关知识.直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1.统计往往和概率进行结合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
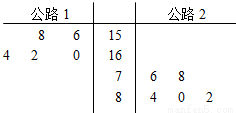
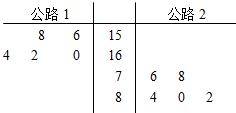 某工厂要将一批产品用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由工厂承担.若工厂恰能在约定日期(×月×日)将产品送到,则销售商一次性支付给工厂2000元;若在约定日期前送到,每提前一天销售商将多支付给工厂100元;若在约定日期后送到,每迟到一天销售商将少支付给工厂100元.现规定汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送产品,现把汽车在一段时间内走公路1和公路2的运费编成如下茎叶图:
某工厂要将一批产品用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由工厂承担.若工厂恰能在约定日期(×月×日)将产品送到,则销售商一次性支付给工厂2000元;若在约定日期前送到,每提前一天销售商将多支付给工厂100元;若在约定日期后送到,每迟到一天销售商将少支付给工厂100元.现规定汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送产品,现把汽车在一段时间内走公路1和公路2的运费编成如下茎叶图:(Ⅰ)写出汽车走公路1和公路2运费的中位数;
(Ⅱ)根据下列信息,
| 统计信息 汽车行驶路线 |
不堵车的情况下到达城市乙所需时间(天) | 堵车的情况下到达城市乙所需时间 (天) | 堵车的概率 | ||
| 公路1 | 2 | 3 |
| ||
| 公路2 | 1 | 4 |
|
求:①以运费的中位数为运费,记汽车走公路1时工厂获得的毛利润为ξ(单位:元),求ξ的分布列和数学期望Eξ;
②假设你是工厂的决策者,你选择哪条公路运送产品有可能让工厂获得的毛利润更多?
某工厂要将一批产品用汽车从所在城市甲运至销售商所在城市乙,已知从城市甲到城市乙只有两条公路,且运费由工厂承担.若工厂恰能在约定日期(×月×日)将产品送到,则销售商一次性支付给工厂2000元;若在约定日期前送到,每提前一天销售商将多支付给工厂100元;若在约定日期后送到,每迟到一天销售商将少支付给工厂100元.现规定汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送产品,现把汽车在一段时间内走公路1和公路2的运费编成如下茎叶图:
(Ⅰ)写出汽车走公路1和公路2运费的中位数;
(Ⅱ)根据下列信息,
(注:毛利润=销售商支付给工厂的费用-运费)
求:①以运费的中位数为运费,记汽车走公路1时工厂获得的毛利润为ξ(单位:元),求ξ的分布列和数学期望Eξ;
②假设你是工厂的决策者,你选择哪条公路运送产品有可能让工厂获得的毛利润更多?
(Ⅰ)写出汽车走公路1和公路2运费的中位数;
(Ⅱ)根据下列信息,
| 统计信息 汽车行驶路线 | 不堵车的情况下到达城市乙所需时间(天) | 堵车的情况下到达城市乙所需时间 (天) | 堵车的概率 |
| 公路1 | 2 | 3 | 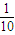 |
| 公路2 | 1 | 4 |  |
求:①以运费的中位数为运费,记汽车走公路1时工厂获得的毛利润为ξ(单位:元),求ξ的分布列和数学期望Eξ;
②假设你是工厂的决策者,你选择哪条公路运送产品有可能让工厂获得的毛利润更多?