题目内容
15.已知A={(x,y)|x+y=2},B={(x,y)|x-y=4},则A∩B=( )| A. | {3,-1} | B. | {x=3,y=-1} | C. | {(3,-1)} | D. | (3,-1) |
分析 联立$\left\{\begin{array}{l}{x+y=2}\\{x-y=4}\end{array}\right.$,解出即可得出.
解答 解:∵集合A={(x,y)|x+y=2},B={(x,y)|x-y=-4},
∴$\left\{\begin{array}{l}{x+y=2}\\{x-y=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,
∴A∩B={(3,-1)},
故选:C.
点评 本题考查了两条直线的交点组成的集合,注意元素的形式,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
3.已知f(x)=-$\frac{1}{3}$x3+2x2+2x,若存在满足-1≤x0≤3的实数x0,使得曲线y=f(x)在点(x0,f(x0))处的切线与直线x+my-10=0垂直,则实数m的取值范围是( )
| A. | [6,+∞) | B. | [-∞,2] | C. | [-3,6] | D. | [5,6] |
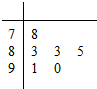 对某同学的6次物理测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法:
对某同学的6次物理测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学物理成绩的以下说法: