题目内容
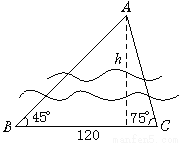
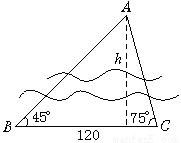
欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB＝45°，∠CBA＝75°，AB＝120 m，求河宽.（精确到0.01 m）
【答案】
河宽94.64米.
【解析】
试题分析：由题意C＝180°－A－B＝180°－45°－75°＝60°
在△ABC中，由正弦定理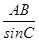
＝
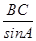
∴ BC＝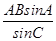
＝
＝
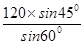＝40
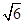
S△ABC＝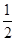
AB·BCsinB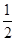＝AB·h
∴h＝BCsinB＝40×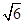
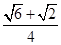＝60＋20
≈94.64
∴河宽94.64米.
考点：本题主要考查正弦定理、三角形内角和定理。
点评：典型题。分析问题的背景，理解题意，灵活选用正弦定理。利用面积求高，图象等积法的灵活运用。
练习册系列答案
相关题目
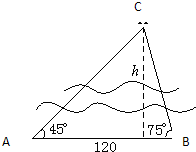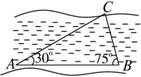
欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB=45°，∠CBA=75°，AB=120m，求河宽．欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB=45°，∠CBA=75°，AB=120m，求河宽．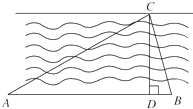
如图，为了测量河的宽度，在一岸边选定两点A，B，望对岸的标记物C，测得∠CAB=30°，∠CBA=75°，AB=120m，则河的宽度是
