题目内容
设n∈N*,n>1,用数学归纳法证明:1+
+
+…+
>
.
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| n |
分析:直接利用数学归纳法的证明步骤证明不等式,(1)验证n=2时不等式成立;(2)假设当n=k(k≥2)时成立,利用放缩法证明n=k+1时,不等式也成立.
解答:证明:记f(n)=1+
+
+…+
.(n∈N*,n>1)…(2分)
(1)当n=2时,f(2)=1+
>
,不等式成立; …(4分)
(2)假设n=k(n∈N*,n≥2)时,不等式成立,…(6分)
即f(k)=1+
+
+…+
>
,
则当n=k+1时,有f(k+1)=f(k)+
>
+
=
>
=
…(10分)
∴当n=k+1时,不等式也成立.…(12分)
综合(1),(2)知,原不等式对任意的n∈N*,(n>1)都成立.…(14分)
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
(1)当n=2时,f(2)=1+
| 1 | ||
|
| 2 |
(2)假设n=k(n∈N*,n≥2)时,不等式成立,…(6分)
即f(k)=1+
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| k |
则当n=k+1时,有f(k+1)=f(k)+
| 1 | ||
|
| k |
| 1 | ||
|
| ||
|
| k+1 | ||
|
| k+1 |
∴当n=k+1时,不等式也成立.…(12分)
综合(1),(2)知,原不等式对任意的n∈N*,(n>1)都成立.…(14分)
点评:本题是中档题,考查数学归纳法的证明步骤,注意不等式的证明方法,放缩法的应用,考查逻辑推理能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

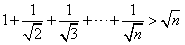 。
。 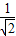 +
+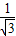 +
+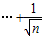
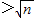 .
.