题目内容
已知集合![]() ,其中
,其中![]() ,
,![]() 表示
表示
![]() 的所有不同值的个数.
的所有不同值的个数.
(1)已知集合![]() ,
,![]() ,分别求
,分别求![]() ,
,![]() ;
;
(2)求![]() 的最小值.
的最小值.
解:(1)由2+4=6,2+6=8,2+8=10,4+6=10,4+8=12,6+8=14,
得l(P)=5
由2+4=6,2+8=10,2+16=18,4+8=12,4+16=20,8+16=24,
得l(Q)=6
(3)不妨设a1<a2<a3<…<an,可得
a1+a2<a1+a3<…<a1+an<a2+an<a3+an<…<an-1+an,
故ai+aj (1≤i<j≤n)中至少有2n-3个不同的数,即l(A)≥2n-3.
事实上,设a1,a2,a3,…,an成等差数列,考虑ai+aj (1≤i<j≤n),根据等差数列的性质,当i+j≤n时, ai+aj=a1+ai+j-1;当i+j>n时, ai+aj=ai+j-n+an;
因此每个和ai+aj(1≤i<j≤n)等于a1+ak(2≤k≤n)中的一个,或者等于al+an(2≤l≤n-1)中的一个.故对这样的集合A,l(A)=2n-3,所以l(A)的最小值为2n-3.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
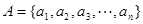 ,其中
,其中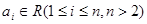 ,
,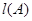 表示和
表示和 中所有不同值的个数.设集合
中所有不同值的个数.设集合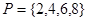 ,则
,则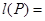 .
.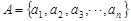 ,其中
,其中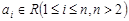 ,
,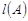 表示
表示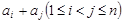 的所有不同值的个数.
的所有不同值的个数.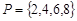 ,
,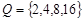 ,分别求
,分别求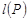 ,
,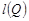 ;
;