题目内容
(本题9分)已知函数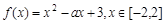 。
。
(Ⅰ)若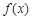 在
在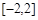 上的最小值是
上的最小值是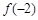 ,试解不等式
,试解不等式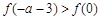 ;
;
(Ⅱ)若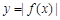 在
在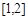 上单调递增,试求实数
上单调递增,试求实数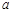 的取值范围。
的取值范围。
【答案】
(Ⅰ)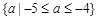 ;(Ⅱ)
;(Ⅱ)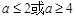 。
。
【解析】
试题分析:(Ⅰ)由已知得 在
在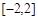 上单调递增,所以
上单调递增,所以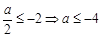 ,
2分
,
2分
又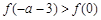 ,所以
,所以 ,
2分
,
2分
所以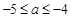 ,即不等式解集为
,即不等式解集为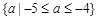 。
1分
。
1分
(Ⅱ)因为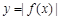 在
在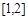 上单调递增,
上单调递增,
所以①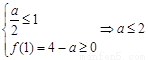 2分
2分
或 ② 2分
2分
综上,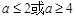 。
。
考点:二次函数的单调性;二次函数的最值;不等式的解法;函数的图像。
点评:数学结合是解决此类的常用方法。我们应熟练掌握函数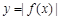 的画法:把
的画法:把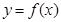 的图像x轴下方的关于x轴翻到x轴上方去即可得
的图像x轴下方的关于x轴翻到x轴上方去即可得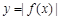 的图像。
的图像。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
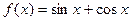 ,
, 是
是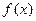 的导函数
的导函数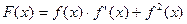 的最小正周期;
的最小正周期;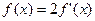 ,求
,求 的值。
的值。 的定义域为集合
的定义域为集合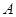 ,
, .
. ,求实数a的取值范围;
,求实数a的取值范围; ,a=
,a= ,求
,求 及
及 .
.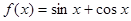 ,
,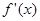 是
是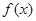 的导函数
的导函数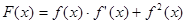 的最小正周期;
的最小正周期;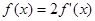 ,求
,求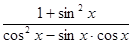 的值。
的值。