题目内容
在△ABC中,设角A,B,C的对边分别为a,b,c,若sinA=sinB=-cosC,
(1)求角A,B,C的大小;
(2)若BC边上的中线AM的长为 ,求△ABC的面积.
,求△ABC的面积.
解:(1)由sinA=sinB知A=B,所以C=π-2A,又sinA=-cosC得,sinA=cos2A,即2sin2A+sinA-1=0,
解得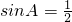 ,sinA=-1(舍). 故
,sinA=-1(舍). 故 ,
,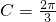 .
.
(2)在△ABC中,由于BC边上中线AM的长为 ,故在△ABM中,由余弦定理得
,故在△ABM中,由余弦定理得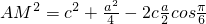 ,
,
即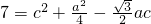 .①
.①
在△ABC中,由正弦定理得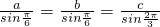 ,即
,即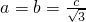 .②
.②
由①②解得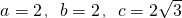 . 故
. 故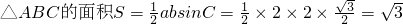 .
.
分析:(1)由正弦定理、二倍角公式结合题中的条件可得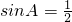 ,故有
,故有 ,
,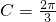 .
.
(2)在△ABM中,由余弦定理得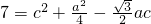 ①,在△ABC中,由正弦定理可得
①,在△ABC中,由正弦定理可得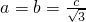 ②,由①②解得
②,由①②解得
a,b,c 的值,即可求得△ABC的面积.
点评:本题考查正弦定理、余弦定理、二倍角公式的应用,求出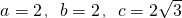 ,是解题的难点.
,是解题的难点.
解得
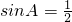 ,sinA=-1(舍). 故
,sinA=-1(舍). 故 ,
,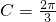 .
.(2)在△ABC中,由于BC边上中线AM的长为
 ,故在△ABM中,由余弦定理得
,故在△ABM中,由余弦定理得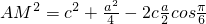 ,
,即
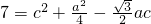 .①
.①在△ABC中,由正弦定理得
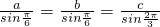 ,即
,即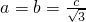 .②
.②由①②解得
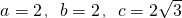 . 故
. 故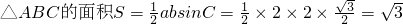 .
.分析:(1)由正弦定理、二倍角公式结合题中的条件可得
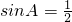 ,故有
,故有 ,
,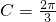 .
.(2)在△ABM中,由余弦定理得
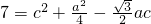 ①,在△ABC中,由正弦定理可得
①,在△ABC中,由正弦定理可得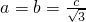 ②,由①②解得
②,由①②解得a,b,c 的值,即可求得△ABC的面积.
点评:本题考查正弦定理、余弦定理、二倍角公式的应用,求出
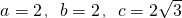 ,是解题的难点.
,是解题的难点. 
练习册系列答案
相关题目