Question

11．在△ABC中，AB=1，∠ABC=60°，$\overrightarrow{AC}$•$\overrightarrow{AB}$=-1，若O是△ABC的重心，则$\overrightarrow{BO}$•$\overrightarrow{AC}$的值为（　　）

• A． 1
• B． $\frac{5}{2}$
• C． $\frac{8}{3}$
• D． 5

Answer 1

分析 建立直角坐标系，利用向量的坐标运算、数量积运算、三角形的重心性质即可得出．

解答 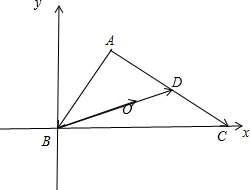解：如图所示，建立直角坐标系．
∵AB=1，∠ABC=60°，
∴A$（\frac{1}{2}，\frac{\sqrt{3}}{2}）$．
设C（a，0）．
∵$\overrightarrow{AC}$•$\overrightarrow{AB}$=-1，
∴$（a-\frac{1}{2}，-\frac{\sqrt{3}}{2}）$•$（-\frac{1}{2}，-\frac{\sqrt{3}}{2}）$=-$\frac{1}{2}（a-\frac{1}{2}）+\frac{3}{4}$=-1，
解得a=4．
∵O是△ABC的重心，
∴$\overrightarrow{BO}$=$\frac{2}{3}\overrightarrow{BD}$
=$\frac{2}{3}×\frac{1}{2}（\overrightarrow{BA}+\overrightarrow{BC}）$
=$\frac{1}{3}[（\frac{1}{2}，\frac{\sqrt{3}}{2}）+（4，0）]$
=$（\frac{3}{2}，\frac{\sqrt{3}}{6}）$．
∴$\overrightarrow{BO}$$•\overrightarrow{AC}$=$（\frac{3}{2}，\frac{\sqrt{3}}{6}）•（\frac{7}{2}，-\frac{\sqrt{3}}{2}）$=5．
故选：D．

点评 本题考查了向量的坐标运算、数量积运算、三角形的重心性质、向量的平行四边形法则等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．