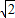题目内容
（重点中学学生做）某校欲在一块长、短半轴长分别为10米与8米的椭圆形土地中规划一个矩形区域搞绿化，则在此椭圆形土地中可绿化的最大面积为（ ）平方米．
分析：先以长轴为x轴，长轴的中垂线为y轴，建立直角坐标系．依题意可知椭圆的标准方程，设矩形第一象限的顶点P的坐标，代入椭圆方程，进而根据均值不等式求得mn的范围，进而根据矩形对称性知面积为S=4mn求得答案．
解答：
解：以长轴为x轴，长轴的中垂线为y轴，建立直角坐标系．依题意可知椭圆的标准方程为
+
=1
不妨设P（m，n）为矩形第一象限的顶点，则
+
=1
由矩形对称性知面积为S=4mn，1=
+
≥2•
∴mn≤40，
∴S≤4×40=160．
则在此椭圆形土地中可绿化的最大面积为160平方米．
故选B．
解：以长轴为x轴，长轴的中垂线为y轴，建立直角坐标系．依题意可知椭圆的标准方程为| x2 |
| 100 |
| y2 |
| 64 |
不妨设P（m，n）为矩形第一象限的顶点，则
| m2 |
| 100 |
| n2 |
| 64 |
由矩形对称性知面积为S=4mn，1=
| m2 |
| 100 |
| n2 |
| 64 |
| mn |
| 10×8 |
∴mn≤40，
∴S≤4×40=160．
则在此椭圆形土地中可绿化的最大面积为160平方米．
故选B．
点评：本题主要考查了椭圆的标准方程及椭圆在实际中的应用．考查了学生对圆锥曲线问题的综合运用．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
某校在筹备校运会时欲制作会徽，准备向全校学生征集设计方案，某学生在设计中需要相同的三角形纸片7张，四边形纸片6张，五边形形纸片9张，而这些纸片必须从A、B两种规格的纸中裁取，具体如下：
（普通中学学生做）若每张A、B型纸的价格分别为3元与4元，试设计一种买纸方案，使该学生在制作时买纸的费用最省，并求此最省费用．
（重点中学学生做）若每张A、B型纸的价格分别为4元与3元，试设计一种买纸方案，使该学生在制作时买纸的费用最省，并求此最省费用．
| 三角形纸片（张） | 四边形纸片（张） | 五边形纸片（张） | |
| A型纸（每张可同时裁取） | 1 | 1 | 3 |
| B型纸（每张可同时裁取） | 2 | 1 | 1 |
（重点中学学生做）若每张A、B型纸的价格分别为4元与3元，试设计一种买纸方案，使该学生在制作时买纸的费用最省，并求此最省费用．
