题目内容
设集X是实数集R上的子集,如果x0∈R满足:对?a>0,都?x∈X,使得0<|x-x0|<a,那么称x0为集合X的聚点,用Z表示整数集,则给出下列集合:
①{
|n∈Z,n≥0};②{x|x∈R,x≠0};③{
|n∈Z,n≠0};④整数集Z
其中以0为聚点的集合的序号有 (写出所有正确集合的序号)
①{
| n |
| n+1 |
| 1 |
| n |
其中以0为聚点的集合的序号有
分析:由已知中关于集合聚点的定义,我们逐一分析四个集合中元素的性质,并判断是否满足集合聚点的定义,进而得到答案.
解答:解:①中,集合{
|n∈Z,n≥0}中的元素是极限为1的数列,
除了第一项0之外,其余的都至少比0大
,
∴在a<
的时候,不存在满足得0<|x|<a的x,
∴0不是集合{
|n∈Z,n≥0}的聚点
②集合{x|x∈R,x≠0},对任意的a,都存在x=
(实际上任意比a小得数都可以),使得0<|x|=
<a
∴0是集合{x|x∈R,x≠0}的聚点
③集合{
|n∈Z,n≠0}中的元素是极限为0的数列,
对于任意的a>0,存在n>
,使0<|x|=
<a
∴0是集合{
|n∈Z,n≠0}的聚点
④对于某个a<1,比如a=0.5,此时对任意的x∈Z,都有|x-0|=0或者|x-0|≥1,也就是说不可能0<|x-0|<0.5,从而0不是整数集Z的聚点
故答案为:②③.
| n |
| n+1 |
除了第一项0之外,其余的都至少比0大
| 1 |
| 2 |
∴在a<
| 1 |
| 2 |
∴0不是集合{
| n |
| n+1 |
②集合{x|x∈R,x≠0},对任意的a,都存在x=
| a |
| 2 |
| a |
| 2 |
∴0是集合{x|x∈R,x≠0}的聚点
③集合{
| 1 |
| n |
对于任意的a>0,存在n>
| 1 |
| a |
| a |
| 2 |
∴0是集合{
| a |
| 2 |
④对于某个a<1,比如a=0.5,此时对任意的x∈Z,都有|x-0|=0或者|x-0|≥1,也就是说不可能0<|x-0|<0.5,从而0不是整数集Z的聚点
故答案为:②③.
点评:本题考查的知识点是集合元素的性质,其中正确理解新定义--集合的聚点的含义,是解答本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
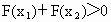 ,求证:
,求证: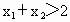 .
.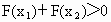 ,求证:
,求证: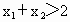 .
. |n∈Z,n≥0};②{x|x∈R,x≠0};③{
|n∈Z,n≥0};②{x|x∈R,x≠0};③{ |n∈Z,n≠0};④整数集Z
|n∈Z,n≠0};④整数集Z