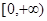题目内容
若函数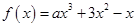 恰有三个单调区间,则实数
恰有三个单调区间,则实数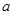 的取值范围为
( )
的取值范围为
( )
A. B.
B. C.
C. D.
D.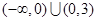
【答案】
C
【解析】
试题分析:由题意知,f′(x)=3ax2+6x-1,
∵f(x)恰有三个单调区间,
∴f′(x)=3ax2+6x-1=0有两个不同的实数根,
∴△=36-4×3a×(-1)>0,且a≠0,即a>-3且a≠0,即(-3,0)∪(0,+∞),故选C.
考点:本题主要考查利用导数研究函数的单调性。
点评:简单题,关键是认识到f′(x)=3ax2+6x-1=0有两个不同的实数根。易错点是忽视对二次项系数的讨论。

练习册系列答案
相关题目
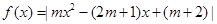 恰有四个单调区间,则实数
恰有四个单调区间,则实数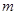 的取值范围( )
的取值范围( )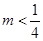 B.
B.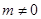 C.
C.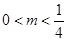 D.
D.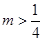
 恰有3个单调区间,则a的取值范围为
恰有3个单调区间,则a的取值范围为
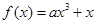 在定义域
在定义域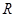 上恰有三个单调区间,则
上恰有三个单调区间,则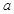 的取值范围是( )
的取值范围是( )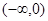 B.
B. C.
C.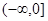 D.
D.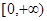
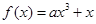 在定义域
在定义域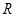 上恰有三个单调区间,则
上恰有三个单调区间,则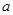 的取值范围是( )
的取值范围是( )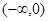 B.
B.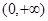 C.
C.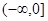 D.
D.