题目内容
函数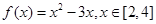 的最大值是 ( )
的最大值是 ( )
| A.-2 | B.4 | C.-3 | D.2 |
B
解析考点:二次函数在闭区间上的最值.
分析:利用二次函数的对称轴公式求出对称轴,根据二次函数的单调性与对称轴有关,判断出函数的单调性,据单调性求出函数的最值.
解:函数的对称轴为x=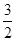
∴f(x)=x2-3x,在[2,4]递增
∴当x=4时,函数有最大值为16-12=4
故选B

练习册系列答案
相关题目
已知函数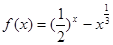 ,那么在下列区间中含有函数
,那么在下列区间中含有函数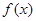 零点的是
零点的是
A.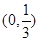 | B.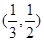 |
C.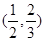 | D.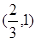 |
函数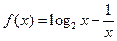 的零点所在区间为
的零点所在区间为
A.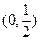 | B.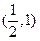 | C.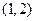 | D.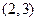 |
在下列函数中,最小值为2的是( )
A.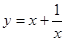 | B.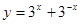 |
C.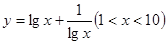 | D.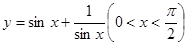 |
.已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,
则
| A.f(33)<f(50)<f(-25) | B.f(50)<f(33)<f(-25) |
C.f (-25)<f(33)<f(50) (-25)<f(33)<f(50) | D.f(-25)<f(50)<f(33) |
函数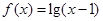 的定义域是
的定义域是
A.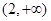 | B.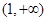 | C.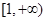 | D.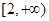 |
已知偶函数 满足
满足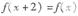 ,且
,且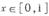 时
时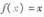 ,则方程
,则方程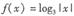 根的个数是
根的个数是
| A.2 | B.3 | C.4 | D.多于 4 |
.已知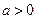 ,且
,且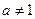 ,
,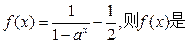
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.奇偶性与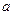 有关 有关 |