题目内容
在正项等比数列{an}中,a1=1,前n项和为Sn,且-a3,a2,a4成等差数列,则S7的值为( ).
| A.125 | B.126 | C.127 | D.128 |
C
解析试题分析:设等比数列{an}的公比为q,由题意可得 q≠1, q3 -q2-2q=0,解得 q=2.
∴S7=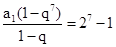 =127,故选C。
=127,故选C。
考点:等比数列的通项公式、求和公式,等差数列的概念。
点评:解答题,思路明确,首先建立公比q的方程,进一步求和。

练习册系列答案
相关题目
已知数列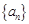 是公比为
是公比为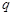 的等比数列,且
的等比数列,且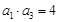 ,
,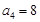 ,则
,则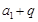 的值为( )
的值为( )
A.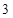 | B.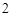 | C.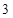 或 或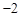 | D.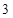 或 或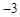 |
在各项都为正数的等比数列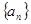 中,首项
中,首项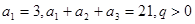 ,则
,则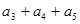 为 ( )
为 ( )
| A.21 | B.4 | C.84 | D.8 |
已知实数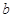 是
是 和
和 的等比中项,则
的等比中项,则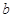 =
=
A. | B.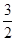 | C. | D.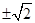 |
已知等比数列的公比是正数,且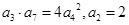 ,则
,则 ( )
( )
A. | B.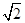 | C. | D. |
已知等比数列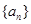 满足
满足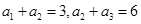 ,则
,则 ( )
( )
| A.64 | B.81 | C.128 | D.243 |
已知实数列-1,x,y,z,-2成等比数列,则xyz等于
| A.-4 | B.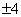 | C.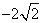 | D.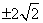 |
若等比数列的首项为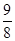 ,末项为
,末项为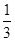 ,公比为
,公比为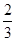 ,则这个数列的项数为( )
,则这个数列的项数为( )
| A.3 | B.4 | C.5 | D.6 |