题目内容
已知椭圆 >b>0)的离心率为
>b>0)的离心率为 ,且过点
,且过点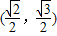 .
.(I)求椭圆的方程;
(II)已知点C(m,0)是线段OF上一个动点(O为原点,F为椭圆的右焦点),是否存在过点F且与x轴不垂直的直线l与椭圆交于A,B两点,使|AC|=|BC|,并说明理由.
【答案】分析:(I)根据椭圆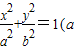 >b>0)的离心率为
>b>0)的离心率为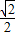 ,且过点
,且过点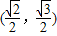 ,建立方程组,即可求得椭圆的方程;
,建立方程组,即可求得椭圆的方程;
(II)设过点F且与x轴不垂直的直线l的方程为:y=k(x-2)代入椭圆方程,消去y可得一元二次方程,求出AB垂直平分线的方程,将C的坐标代入,即可求得结论.
解答:解:(I)由题意,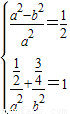 ,∴
,∴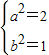 ,∴椭圆的方程为
,∴椭圆的方程为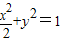 ;
;
(II)设过点F且与x轴不垂直的直线l的方程为:y=k(x-2)代入椭圆方程,消去y可得
(1+2k2)x2-8k2x+8k2-2=0,则△=16k4-4(1+2k2)(8k2-2)=-16k2+8>0,∴k2<
设A(x1,y1),B(x2,y2),则x1+x2=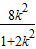 ,y1+y2=-
,y1+y2=-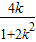
∴AB的中点的坐标为( )
)
∴AB的垂直平分线的方程为y+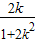 =-
=-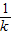 (x-
(x-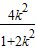 )
)
将点C(m,0)代入可得0+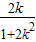 =-
=-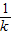 (m-
(m-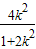 )
)
∴m=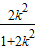
∵0<m<2
∴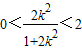 恒成立
恒成立
∴存在过点F且与x轴不垂直的直线l与椭圆交于A,B两点,使|AC|=|BC|.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,确定椭圆的方程,求出AB的垂直平分线的方程是关键.
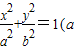 >b>0)的离心率为
>b>0)的离心率为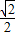 ,且过点
,且过点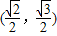 ,建立方程组,即可求得椭圆的方程;
,建立方程组,即可求得椭圆的方程;(II)设过点F且与x轴不垂直的直线l的方程为:y=k(x-2)代入椭圆方程,消去y可得一元二次方程,求出AB垂直平分线的方程,将C的坐标代入,即可求得结论.
解答:解:(I)由题意,
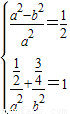 ,∴
,∴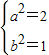 ,∴椭圆的方程为
,∴椭圆的方程为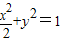 ;
;(II)设过点F且与x轴不垂直的直线l的方程为:y=k(x-2)代入椭圆方程,消去y可得
(1+2k2)x2-8k2x+8k2-2=0,则△=16k4-4(1+2k2)(8k2-2)=-16k2+8>0,∴k2<

设A(x1,y1),B(x2,y2),则x1+x2=
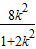 ,y1+y2=-
,y1+y2=-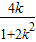
∴AB的中点的坐标为(
 )
)∴AB的垂直平分线的方程为y+
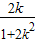 =-
=-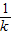 (x-
(x-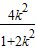 )
)将点C(m,0)代入可得0+
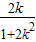 =-
=-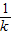 (m-
(m-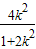 )
)∴m=
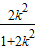
∵0<m<2
∴
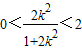 恒成立
恒成立∴存在过点F且与x轴不垂直的直线l与椭圆交于A,B两点,使|AC|=|BC|.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,确定椭圆的方程,求出AB的垂直平分线的方程是关键.

练习册系列答案
相关题目
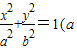 >b>0)的离心率为
>b>0)的离心率为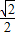 ,且过点
,且过点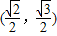 .
.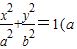 >b>0)的离心率为
>b>0)的离心率为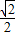 ,且过点
,且过点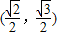 .
. >b>0)的离心率为
>b>0)的离心率为 ,且过点
,且过点 .
.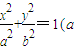 >b>0)的离心率为
>b>0)的离心率为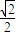 ,且过点
,且过点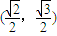 .
.