题目内容
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=- 对称,且f′(1)=0
对称,且f′(1)=0(Ⅰ)求实数a,b的值
(Ⅱ)求函数f(x)的极值.
【答案】分析:(Ⅰ)先对f(x)求导,f(x)的导数为二次函数,由对称性可求得a,再由f′(1)=0即可求出b
(Ⅱ)对f(x)求导,分别令f′(x)大于0和小于0,即可解出f(x)的单调区间,继而确定极值.
解答:解:(Ⅰ)因f(x)=2x3+ax2+bx+1,故f′(x)=6x2+2ax+b
从而f′(x)=6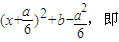 y=f′(x)关于直线x=-
y=f′(x)关于直线x=-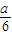 对称,
对称,
从而由条件可知-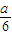 =-
=- ,解得a=3
,解得a=3
又由于f′(x)=0,即6+2a+b=0,解得b=-12
(Ⅱ)由(Ⅰ)知f(x)=2x3+3x2-12x+1
f′(x)=6x2+6x-12=6(x-1)(x+2)
令f′(x)=0,得x=1或x=-2
当x∈(-∞,-2)时,f′(x)>0,f(x)在(-∞,-2)上是增函数;
当x∈(-2,1)时,f′(x)<0,f(x)在(-2,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上是增函数.
从而f(x)在x=-2处取到极大值f(-2)=21,在x=1处取到极小值f(1)=-6.
点评:本题考查函数的对称性、函数的单调区间和极值,考查运算能力.
(Ⅱ)对f(x)求导,分别令f′(x)大于0和小于0,即可解出f(x)的单调区间,继而确定极值.
解答:解:(Ⅰ)因f(x)=2x3+ax2+bx+1,故f′(x)=6x2+2ax+b
从而f′(x)=6
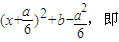 y=f′(x)关于直线x=-
y=f′(x)关于直线x=-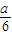 对称,
对称,从而由条件可知-
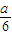 =-
=- ,解得a=3
,解得a=3又由于f′(x)=0,即6+2a+b=0,解得b=-12
(Ⅱ)由(Ⅰ)知f(x)=2x3+3x2-12x+1
f′(x)=6x2+6x-12=6(x-1)(x+2)
令f′(x)=0,得x=1或x=-2
当x∈(-∞,-2)时,f′(x)>0,f(x)在(-∞,-2)上是增函数;
当x∈(-2,1)时,f′(x)<0,f(x)在(-2,1)上是减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上是增函数.
从而f(x)在x=-2处取到极大值f(-2)=21,在x=1处取到极小值f(1)=-6.
点评:本题考查函数的对称性、函数的单调区间和极值,考查运算能力.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 对称,且f′(1)=0
对称,且f′(1)=0 对称,且f′(1)=0
对称,且f′(1)=0