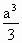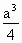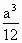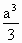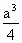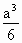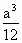题目内容
(2003年新课程卷)棱长为a有正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为
[ ]
|
A. |
B. |
C. |
D. |
答案:C
解析:
解析:
|
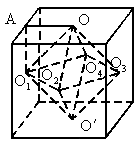
解:如图所示,  是正方体四个侧面正方形的中心,O、是上、下两个底面正方形的中心,每相邻两个中心的连线长度相等. 是正方体四个侧面正方形的中心,O、是上、下两个底面正方形的中心,每相邻两个中心的连线长度相等.
设 A为棱的中点,则△ 是等腰直角三角形,且 是等腰直角三角形,且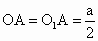 . .
∴ 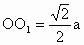 . .
由题意,正四棱锥 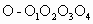 的高应为正方体棱长的一半,即 的高应为正方体棱长的一半,即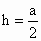 , ,
又正方形 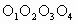 的面积 的面积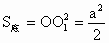 . .
∴ 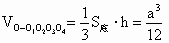 . .
∴八面体的体积应等于 2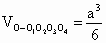 .∴选C. .∴选C.
每相邻两个面貌一新的中心连线长为 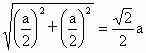 .该八面体的各个面都是全等的正三角形,且 .该八面体的各个面都是全等的正三角形,且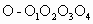 是棱长都相等的正四棱锥,据此便可计算出该八面体的体积. 是棱长都相等的正四棱锥,据此便可计算出该八面体的体积. |

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目