题目内容
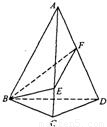
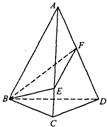如图，已知正三棱锥A-BCD侧面的顶角为40°，侧棱长为a，动点E、F分别在侧棱AC、AD上，则以线段BE、EF、FB长度和的最小值为半径的球的体积为（ ）A、4
| ||
B、
| ||
C、
| ||
| D、4πa3 |
分析：要求BE+EF+FB的最小值，将三棱锥展开，如图，求出线段BG长度，再求球的体积即可．
解答：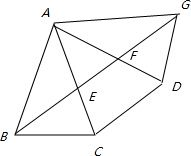
解：将三棱锥展开如图，则BE+EF+FB的最小值，
就是图中BG的长，∠BAG=120°，AB=a，
所以BG=
a，所以球的半径是
a，
球的体积是：
(
a)3 =4
πa3，
故选A．
解：将三棱锥展开如图，则BE+EF+FB的最小值，就是图中BG的长，∠BAG=120°，AB=a，
所以BG=
| 3 |
| 3 |
球的体积是：
| 4π |
| 3 |
| 3 |
| 3 |
故选A．
点评：本题考查棱锥的侧面展开图，球的体积，考查学生发现问题解决问题的能力，计算能力，是基础题．
练习册系列答案
相关题目
