题目内容
在n行n列矩阵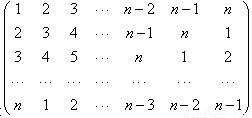 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .
【答案】分析:因为n=9,得到九行九列矩阵并写出矩阵,由于第i行第j列的数为aij,则a11=1,a22=3,a33=5,a44=7,a55=9,a66=2,a77=4,a88=6,a99=8求出之和即可.
解答:解:根据题意,由于第i行第j列的数为aij,
则a11=1,a22=3,a33=5,a44=7,a55=9,a66=2,a77=4,a88=6,a99=8;
故a11+a22+a33+…+a99=1+3+5+7+9+2+4+6+8=45.
故答案为:45.
点评:本题考查学生对高阶矩阵的表示和理解运用计算的能力.
解答:解:根据题意,由于第i行第j列的数为aij,
则a11=1,a22=3,a33=5,a44=7,a55=9,a66=2,a77=4,a88=6,a99=8;
故a11+a22+a33+…+a99=1+3+5+7+9+2+4+6+8=45.
故答案为:45.
点评:本题考查学生对高阶矩阵的表示和理解运用计算的能力.

练习册系列答案
相关题目
 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99=
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= 中,记位于第i行第j列的数为aij(i,j=1,2,…,n).当n=9时,a11+a22+a33+…+a99=________.
中,记位于第i行第j列的数为aij(i,j=1,2,…,n).当n=9时,a11+a22+a33+…+a99=________.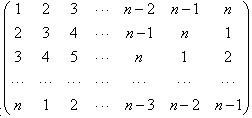 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99=________.
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99=________.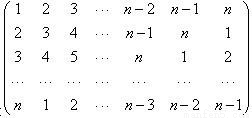 中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .
中,记位于第i行第j列的数为aij(i,j=1,2…,n).当n=9时,a11+a22+a33+…+a99= .