题目内容
在极坐标系中,点A在曲线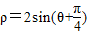 上,点B在直线ρcosθ=-1上,则|AB|的最小值是 .
上,点B在直线ρcosθ=-1上,则|AB|的最小值是 .
【答案】分析:曲线 表示以(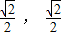 ) 为圆心,以1为半径的圆,直线ρcosθ=-1 即 x=-1,圆心到直线的距离等于 1+
) 为圆心,以1为半径的圆,直线ρcosθ=-1 即 x=-1,圆心到直线的距离等于 1+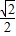 ,|AB|的最小值是 此距离减去半径.
,|AB|的最小值是 此距离减去半径.
解答:解:曲线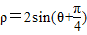 即 ρ2=2×
即 ρ2=2×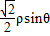 +2×
+2×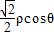 ,即 x2+y2-
,即 x2+y2-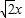 -
-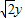 =0,
=0,
表示以(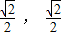 ) 为圆心,以1为半径的圆. 直线ρcosθ=-1 即 x=-1.
) 为圆心,以1为半径的圆. 直线ρcosθ=-1 即 x=-1.
圆心到直线的距离等于 1+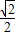 ,|AB|的最小值是 (1+
,|AB|的最小值是 (1+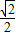 )-1=
)-1=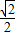 ,
,
故答案为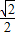 .
.
点评:本题考查把极坐标方程化为直角坐标方程的方法,求点到直线的距离,求出圆心到直线的距离等于 1+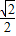 ,是解题的关键.
,是解题的关键.
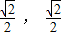 ) 为圆心,以1为半径的圆,直线ρcosθ=-1 即 x=-1,圆心到直线的距离等于 1+
) 为圆心,以1为半径的圆,直线ρcosθ=-1 即 x=-1,圆心到直线的距离等于 1+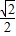 ,|AB|的最小值是 此距离减去半径.
,|AB|的最小值是 此距离减去半径.解答:解:曲线
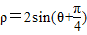 即 ρ2=2×
即 ρ2=2×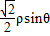 +2×
+2×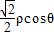 ,即 x2+y2-
,即 x2+y2-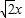 -
-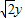 =0,
=0,表示以(
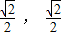 ) 为圆心,以1为半径的圆. 直线ρcosθ=-1 即 x=-1.
) 为圆心,以1为半径的圆. 直线ρcosθ=-1 即 x=-1.圆心到直线的距离等于 1+
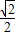 ,|AB|的最小值是 (1+
,|AB|的最小值是 (1+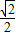 )-1=
)-1=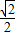 ,
,故答案为
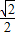 .
.点评:本题考查把极坐标方程化为直角坐标方程的方法,求点到直线的距离,求出圆心到直线的距离等于 1+
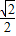 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
 上,点B在曲线ρcosθ=-1上,则|AB|的最小值是
上,点B在曲线ρcosθ=-1上,则|AB|的最小值是

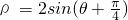 上,点B在直线ρcosθ=-1上,则|AB|的最小值是________.
上,点B在直线ρcosθ=-1上,则|AB|的最小值是________.